1.设计变量

根据加强圈的实际情况和设计特点，选定A_s、D_s和L_s作为优化的设计变量。即

2.目标函数

以最小质量为加强圈的设计目标，则目标函数的数学表达式可写为

f（X）=πA_sD_sρ （9-40）

式中 ρ——材料密度（kg/m³）；

D_s——加强圈截面中性轴直径（mm）；

A_s——个加强圈的截面积（mm²）；

将π值代入上式，并以x₁、x₂分别取代A_s、D_s，则上式可写成：

f（X）=3.14x₁x₂ρ （9-41）

3.约束条件

确定约束条件的依据是对加强圈刚度条件的要求和其他相关结构、尺寸等方面的限制。可从以下几个方面考虑：

（1）加强圈的刚度条件 外压圆筒设计的加强圈与外压筒体两则有效段组成的惯性矩：

应满足以下刚度要求，即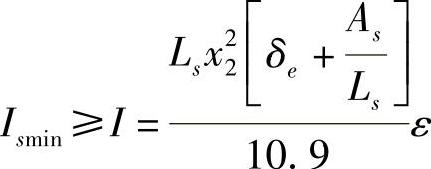

依上述分析得约束条件：

式中 ε——应变；

I——加强圈与壳体组合段所需的惯性矩（mm⁴）；

δ_e——外压圆筒的计算厚度（mm）；

L_s——计算长度（mm）；

I₁——加强圈对其形心轴x₁-x₂的惯性矩（mm⁴）；

a₁——加强圈形心轴至组合截面形心轴x-x的距离（mm）；

I₂——外压圆筒截面对其形心轴x₂-x₂的惯性矩（mm⁴）；

a₂——组合截面形心轴x-x至圆筒截面形心轴x₂-x₂的距离（mm）；

A_c——外压圆筒有效宽度b内的截面积（mm²），A_c=2bδ_e；(www.daowen.com)

b——外压圆筒的有效宽度（mm），取b=0.55。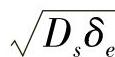

（2）加强圈截面积约束条件 加强圈截面积A_s应在各类型材面积规格范围内，即

A_smin≤As≤Asmax

故约束条件为

g₂（X）=A_smin-x₁≤0 （9-43）

g₃（X）=x₁-A_smax≤0 （9-44）

（3）加强圈最大间距条件 外压圆筒上加强圈最大间距的限制，若加强圈之间的最大间距用下式确定：

只有当加强圈的实际间距L_s≤L_max时，外压圆筒才能安全承受设计外压p。故约束条件为

式中 δ_e——外压圆筒的有效厚度（mm）；

E——材料的弹性模量（MPa）；

m——外压圆筒的稳定系数；

p——设计外压力（MPa）；

D_o——外压圆筒的外直径（mm）（此处近似用加强圈截面中性轴直径D_s代替）。

（4）加强圈在筒体上安放位置的尺寸限制 对同一种型钢，在外压圆筒器壁上无论采用何种安放形式，其加强圈截面中性轴直径D_s应受到外压圆筒直径S_i（或D_o）规定值的限制。即

D_imin≤Ds≤Dimax

故约束条件为

g₅（X）=D_imin-x₂≤0 （9-46）

g₆（X）=x₂-D_imax≤0 （9-47）

综上所述，最小质量外压容器加强圈优化设计的数学模型概括为如下形式：

minf（X）=3.14x₁x₂ρ

约束条件：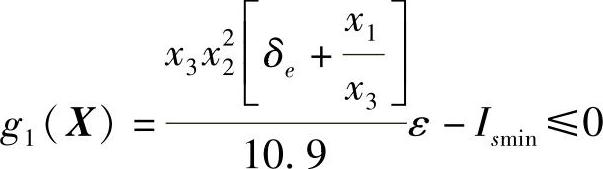

由以上各式表明，该问题为具有多个不等式约束条件的三维非线性数学规划问题。