1.数学模型

可靠性优化设计一般有两种方法：以可靠度为约束条件，使其他设计指标如成本、质量、尺寸等为最优；或以成本、质量及其他设计指标为约束条件，使设计对象的可靠度达到最优。在可靠性设计中，常常预先规定产品的可靠度指标β^*（或R_e^*）。本节采用前一种方法对有加强圈外压薄壁圆筒进行可靠性优化设计，即以可靠度指标β^*（或R_e^*）为约束条件，使筒体质量为最轻，其数学模型的一般形式为

f（X）=minG

约束条件：β（X）≥β^*

g_j（X）≥0 （j=1，2，…，i）

式中 f（X）——目标函数；

G——筒体质量；

β^*——规定可靠度指标；

β（X）——可靠度指标函数；

g_j（X）——约束条件。

（1）设计变量 本节以用扁钢为加强圈的壳体为例，进行可靠性优化设计，其结构主要由筒体总长L、筒体内半径R、筒壁厚度x₁、加强圈间距x₂、加强圈高度x₃、加强圈宽度x₄6个参数确定如图9-2所示。

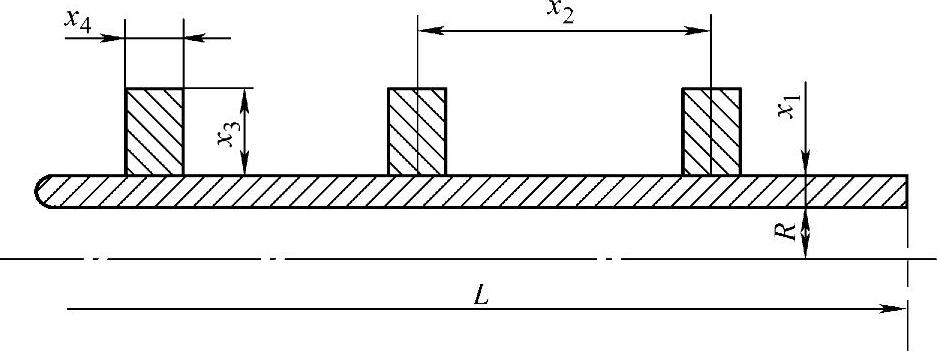
图9-2 筒体结构简图

在实际设计中，筒体总长、筒体内半径为工艺设计时给定，因此结构设计变量为x₁～x₄。即

X=（x₁，x₂，x₃，x₄）^T （9-31）

（2）目标函数

f（X）=f₁（X）+f₂（X） （9-32）

式中 f₁（X）——壳体质量。

f₁（X）=[π（R+x₁）2-πR²]Lρ （9-33）

f₂（X）——加强圈质量。

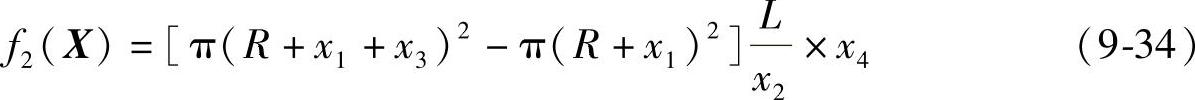
式中 ρ——材料密度（kg/m³）。

（3）约束条件

1）可靠度约束。选取可靠度指标β^*=4.265（即R_e^*=0.99999）

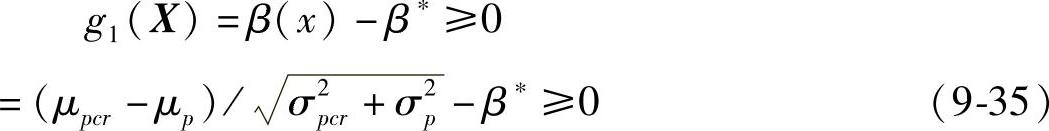(www.daowen.com)

2）尺寸约束。在结构设计过程中，其尺寸参数一般是给定一个大小取值范围，设尺寸参数x_i最小取值为x_imin，最大取值为x_imax，则尺寸参数x_i的优化取值范围为x_imin≤x≤x_imax，故

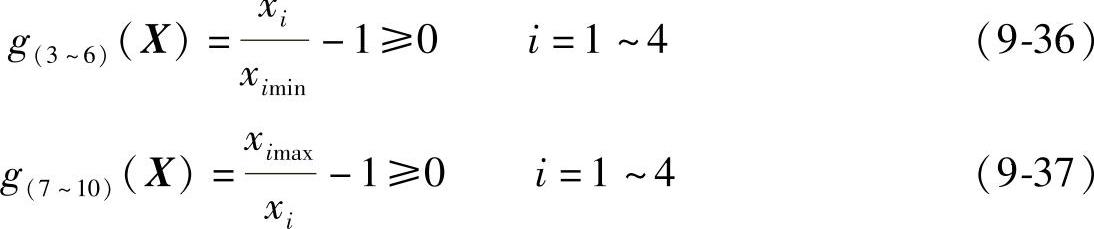
3）其他约束。每一个加强圈（包括部分壳体）应能承受分布于加强圈间距上的全部载荷而不失稳，其约束为

式中 J——加强圈与壳壁的综合截面惯性矩（mm⁴）。

2.优化方法及参数圆整

上述优化设计数学模型是四维非线性规划问题，有11个约束条件，采用复合型优化方法较为合适。在本优化设计中，设计变量壳体壁厚、加强圈型钢尺寸需按标准系列取值，为离散数，而加强圈间距则需要取为整型量。对于这种特殊问题，在优化计算时，先将所有设计变量作为连续变量处理，在求得最优解以后，再对要求按标准系列取值的设计变量和要求为整型量的设计变量作圆整处理。其计算程序框图如图9-3所示。

3.优化实例与结果分析

（1）已知条件 一减压塔，采用扁钢作加强圈，材料采用16MnR，设计参数如下：

设计压力p（μ_p，σ_p）=（0.1，0.0017）MPa

材料屈服点σ_s（μσ_s，σσ_s）=（321，23）MPa

弹性模量E（μ_E，σ_E）=（1.97×10⁵，5.93×10³）MPa

总长度（包括封头直边）L（_μL，σ_L）=（24000，24）mm

内半径R（μ_R，σ_R）=（1200，1.2）mm

x_i的取值范围：6≤x₁≤12，2200≤x₂≤3500，75≤x₃≤100，15≤x₄≤22

（2）优化结果（圆整值）优化结果的圆整值为

X=（x₁，x₂，x₃，x₄）^T=（8，3000，80，16）^T

而按常规设计结果为

X=（10，2400，90，20）^T

可见，本例采用可靠性优化设计壳体的质量比按常规设计的质量约降低21.7%，且可靠度可达0.999990。

从以上可靠性优化设计结果可知，在满足可靠度要求的条件下，结构可靠性优化设计具有使结构质量减轻、尺寸合理的优点，对压力容器尺寸结构采用可靠性优化设计不失为一种好的有效的设计方法。

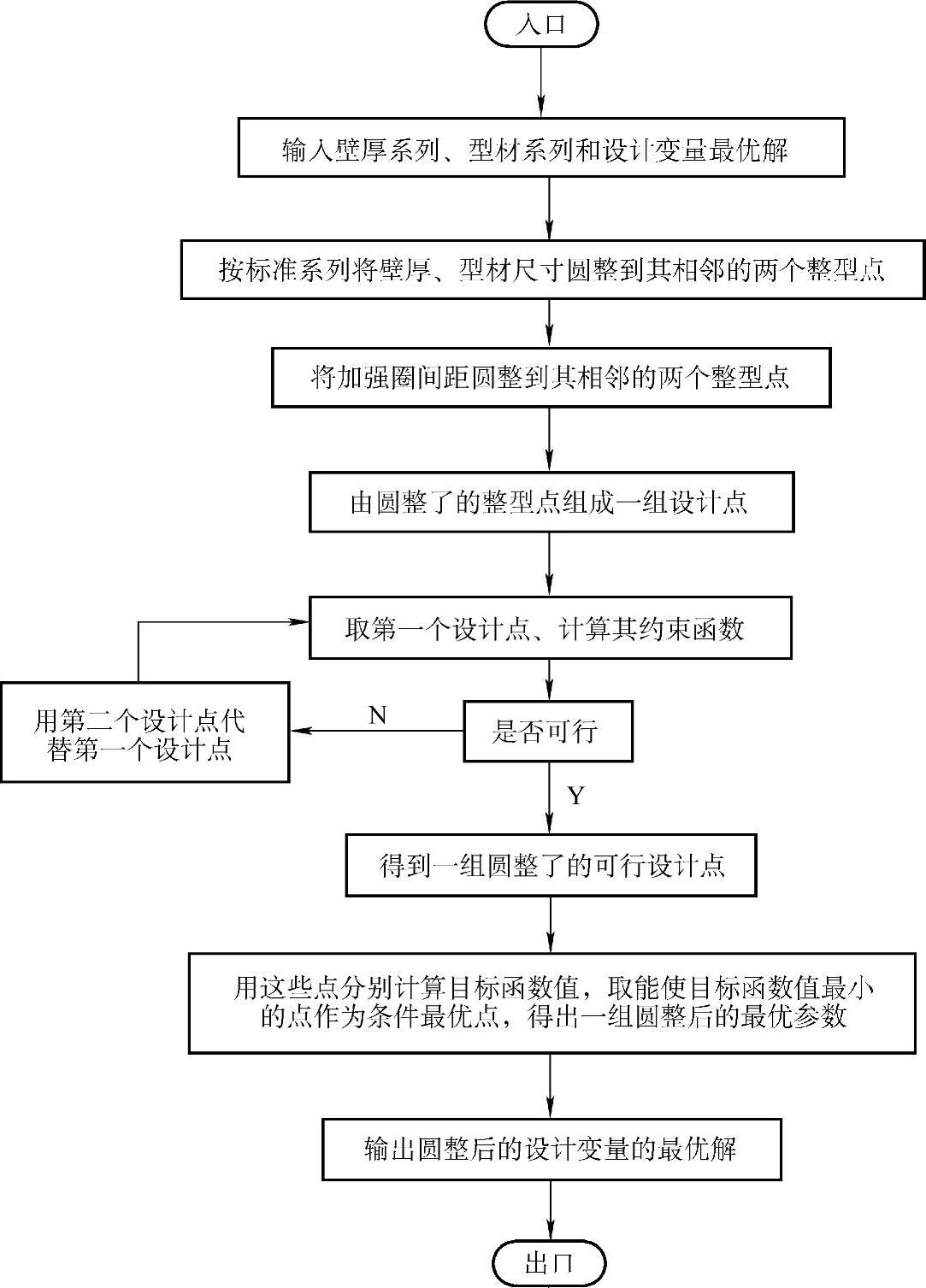
图9-3 参数圆整计算程序框图