1.失效模式及应力分布

有加强圈圆筒在承受外压时，筒体可能发生某种形式的失效：

1）段内筒体因强度不足而导致破坏。

2）段内筒体失稳破坏。

3）筒体总体失稳破坏。

理论分析及长期工程实践证明，有加强圈外压薄壁圆筒的失效主要是段内筒体失稳。失稳时，壳体的压缩应力一般低于材料的比例极限，属弹性失稳。因此可得段内筒体失稳时的临界压力：

式中 E——筒体材料弹性模量（MPa）；

μ——泊松比；

δ——筒体壁厚（mm）；

R——筒体内半径（mm）；

L₁——加强圈间距（mm）；

n——失稳波数，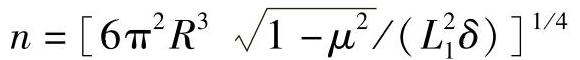

段内筒体失稳时，加强圈应力：

σ_q=-k_qpR/t （9-26）(www.daowen.com)

k_q=0.85[1-k_m（sh（2u）+usin2）]

式中 k_q——应力修正系数；

p——筒体所受外压；

A_q——加强圈截面积。

对于由独立随机变量x_i（i=1，2，…，m）组成的变量z=f（x₁，x₂，…，x_m），m为独立随机变量数，若设随机变量x_i的平均值为μ_i，标准离差为σ_i，则组合变量z的平均值和标准离差可由下式计算：

μ_z=f（μ₁，μ₂，…，μm） （9-27）

筒体临界压力均值_μpcr和标准离差σ_pcr，加强圈应力均值μ_q和标准离差σ_σq均可由式（9-27）和式（9-28）计算。

2.可靠度计算

设筒体强度和应力均服从正态分布，结构可靠度指标可由下式计算：

式中 μ_r、μ_s——分别为屈服强度和失效应力均值；

σ_r、σ_s——分别为屈服强度和失效应力的标准离差。

从失效模式分析已知，当圆筒操作外压达到临界压力值时将引起失稳。设操作外压p和临界压力p_cr呈正态全布。在此，只要把p_cr看作强度，把p看作应力，即可用式（9-29）计算有加强圈外压薄壁圆筒结构可靠度指标：

将已知数据代入式（9-30）算出可靠度指标β，根据β值查正态分布表即可求出圆筒的可靠度值R_e。