1.数学模型

（1）目标函数 根据前面分析，外压薄壁圆筒壁厚的设计关键在于确定p_cr，使其大于设计压力p。考虑经济问题，应使p_cr/mp尽量小，所以衡量指标为p_cr/mp。于是确定目标函数为

f（X）=p_cr/mp （9-4）

基于Misses公式，外压薄壁圆筒壁厚优化设计的目标函数为

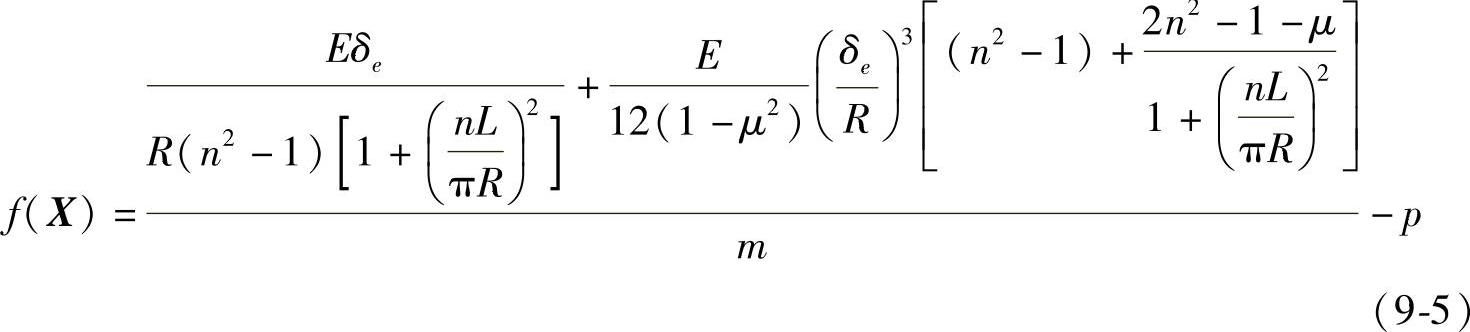
（2）约束条件 本优化设计数学模型包含不等式约束和等式约束。

1）不等式约束。稳定性条件：

g₁（X）=f（X）≥0 （9-6）

最小壁厚条件：

g₂（X）=δ_e-3≥0 （9-7）

薄壁条件：

g₃（X）=0.2-δ_e/R≥0 （9-8）

2）等式约束

h₁（X）=E-const1=0 （9-9）

h₂（X）=R-const2=0 （9-10）

h₃（X）=L-const3=0 （9-11）

h₄（X）=μ-const4=0 （9-12）

h₅（X）=m-const5=0 （9-13）

h₆（X）=p-const6=0 （9-14）

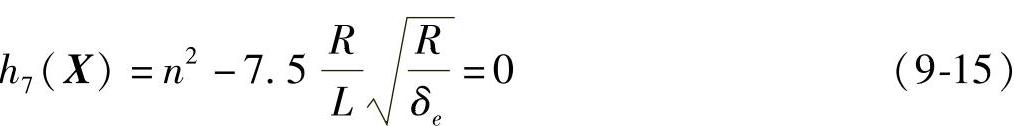
同理，基于邵斯威尔公式，目标函数可表达为

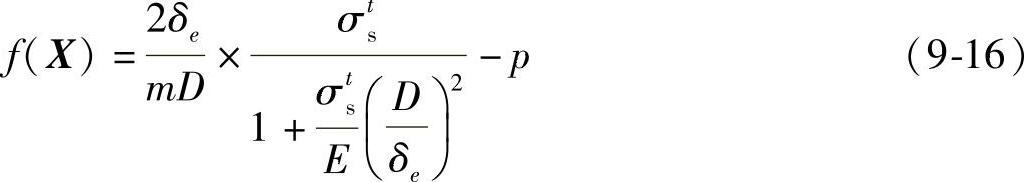
同样地，具有如下不等式和等式约束。

1）不等式约束。稳定性条件：

g₁（X）=f（X）≥0 （9-17）

最小壁厚条件：

g₂（X）=S₀-3≥0 （9-18）

薄壁条件：

g₃（X）=0.2-S₀/R≥0 （9-19）

2）等式约束

h₁（X）=D-const1=0 （9-20）

h₂（X）=E-const2=0 （9-21）(www.daowen.com)

h₃（X）=m-const3=0 （9-22）

h₄（X）=p-const4=0 （9-23）

h₅（X）=σ^t_s-const5=0 （9-24）

等式约束中const1～6分别代表6个不同常量。至此，薄壁圆筒壁厚设计的数学模型已建立。对模型进行分析知，基于Misses公式的数学模型有8个设计参数，其中7个为常量；基于邵斯威尔公式的数学模型有6个设计参数，其中5个为常量。所以无论是采用Misses公式还是采用邵斯威尔公式，都属于最优化设计中的一维搜索问题，其设计变量都只有一个，即壁厚δ_e。

2.优化方法

由以上分析知，δ_e的值域为[3，0.2p]，数学模型为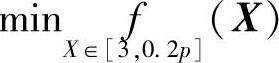，受约束为g₁（X）=f（X）≥0，所以问题最后可归结为求方程f（X）=0的近似解。在一维搜索问题的最优化方法中，考虑收敛速度问题，这里选用切线法。

切线法原理如图9-1所示。

1）先在区间[a，b]内选取a^（0）为a^*的初始近似值，在曲线y=f（X^（k）+aS^（k））上经过点[a^（0），f（X^（k）+aS^（k））]的切线方程为y=f（a^（0））+f′（a^（0））（a+a^（0））。而切线与a轴的交点为：

。

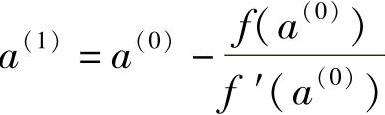2）当f（a^（1））≠0时，再由点[a^（1），f（X^（k）+a^（1）S^（k））]作曲线y=f（a）的切线，与a轴相交，得交点：

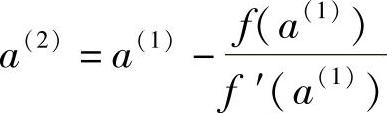
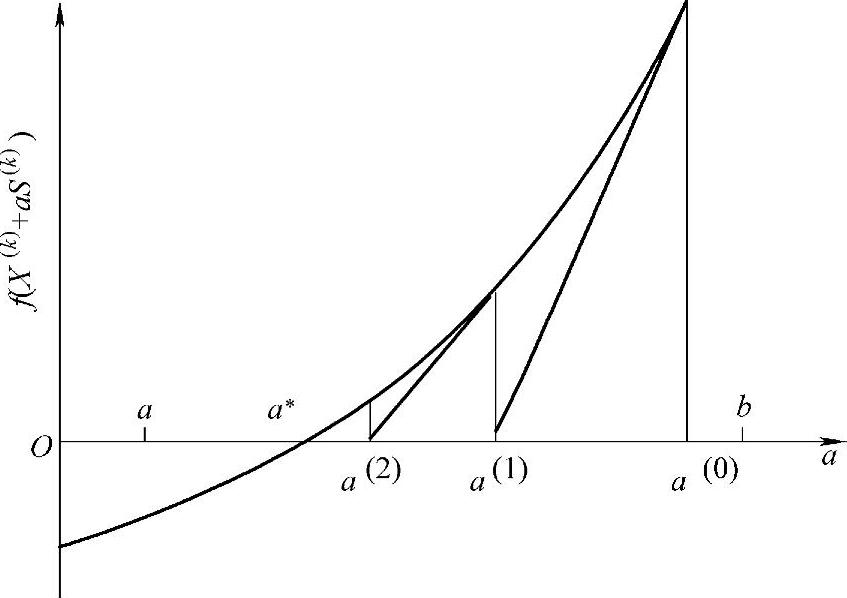
图9-1 切线法原理

3）重复上述步骤，经过有限次迭代，得到点列a（0），a（1），a（2），…，a（k）。当k足够大时，满足a^（k-1）-a^（k）≤δ或f（a^（k-1））≤ε。则认为a^（k）是a^*的近似值。

上述式中δ和ε是给定的允许误差，且δ和ε均大于0。

3.优化设计实例

【例9-1】 已知一分馏塔，经工艺计算塔内径D_i=2000mm，计算长度L=6140mm，在370℃及真空下操作，选用20g钢板制造，试确定有加强圈时塔身壁厚（注：20g在370℃时，E=1.73×10⁵MPa，σ^t_s=161MPa，选取壁厚附加量C=2mm）。

解：根据已知条件可确定壁厚S₀的值域为[3，200]，具体计算过程如下：

第1次计算：δ_e=200.000000f（X）=155.012236

第2次计算：δ_e=129.645691f（X）=46.787310

第3次计算：δ_e=80.989845f（X）=14.377036

第4次计算：δ_e=46.168400f（X）=4.507952

第5次计算：δ_e=30.606565f（X）=1.326078

第6次计算：δ_e=20.409033f（X）=0.378043

第7次计算：δ_e=14.163162f（X）=0.095531

第8次计算：δ_e=11.147129f（X）=0.015993

第9次计算：δ_e=10.402397f（X）=0.000808

第10次计算：δ_e=10.360613f（X）=0.000002

最后结果：δ_e=10.360613f（X）=0.000002

上述优化设计实例结果表明，采用切线法收敛速度很快，具体迭代次数可由允许误差δ和ε控制，结果令人满意。