利用ANSYS提供的APDL语言，进行参数化建模，并利用其OPT模块进行寻优，确定锻件的合理结构尺寸。

1.有限元计算模型

计算采用轴对称模型（图8-7），模型中考虑了整体补强锻件与球壳的焊接结构，接管长度及球壳部分沿经线方向的长度均远大于各自的衰减长度。选用8节点4边形单元Plane82，共划分793个单元。材料的弹性模量取为2×10⁵MPa，泊松比取为0.3。接管端部约束轴向位移，球壳端部以面力p₁模拟封闭球罐的受力情况。

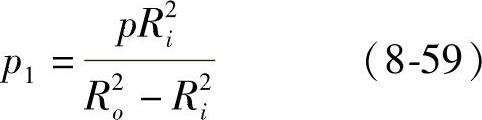
式中 R_i、R_o——球壳的内、外半径（mm）。

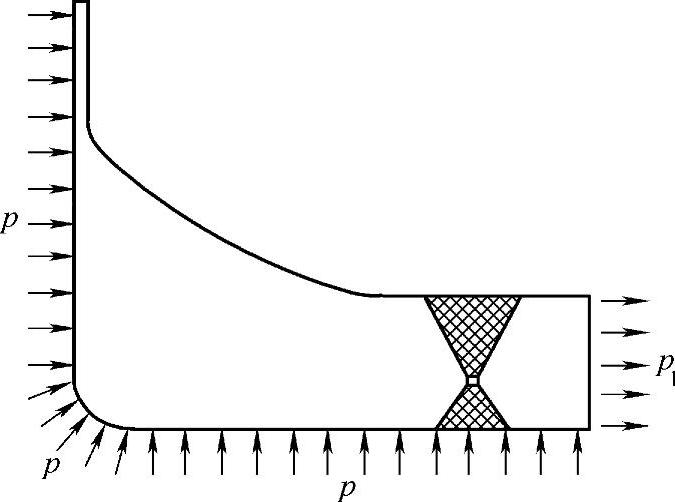
图8-7 有限元计算模型

2.基于分析设计的准等强度原则的优化数学模型

基于分析设计的准等强度原则可有效地对上述结构进行优化设计。令球壳总体薄膜应力的应力强度水平系数为

式中 σ_m——球壳总体薄膜应力强度，

图8-8 应力评定路径图

α——应力强度水平系数，取α=0.829。(www.daowen.com)

在选定的12条应力评定路径上（图8-8所示其中路径L₅为内圆角处最大应力点和该点到锻件外端面最短距离点的连线，路径L₆为双锥段外过渡圆角处最大应力点和该点到锻件内表面最短距离点的连线）。利用ANSYS提供的关于路径的线性化处理程序可得到每条应力评定路径上的薄膜应力、弯曲应力以及峰值应力。根据球壳接管区域在内压作用下应力的性质，薄膜应力可划为一次局部薄膜应力，弯曲应力划为二次应力。局部薄膜应力的应力强度水平系数为

一次应力加二次应力的应力强度水平系数为

根据基于分析设计的准等强度原则，应力强度水平系数应满足如下条件：

β≤α （8-63）

ξ≤α

于是，对于上述问题可建立如下优化数学模型：

（1）设计变量

X=[x₁，x₂，x₃，x₄，x5，x6]^T=[R₁，R2，r1，r2，α1，α2]^T （8-64）

（2）约束条件 由几何尺寸的约束要求δ/8≤r₁≤δ/2，δ/8≤r₂≤δ/2，α₁≤30°，α₂≤45°，β，ξ≤α，可得相应的约束条件如下：

（3）目标函数 以整体补强锻件子午面面积A最小为优化目标，并构建目标函数。该面积可计算得到，也可利用ANSYS中的get命令提取。