设计一个带球形封头的等壁厚卧式圆筒型储罐。要求在容积不变的条件下，求取最大应力不超过许用应力而质量为最轻的筒体直径D、长度L及壁厚δ（图8-1）。

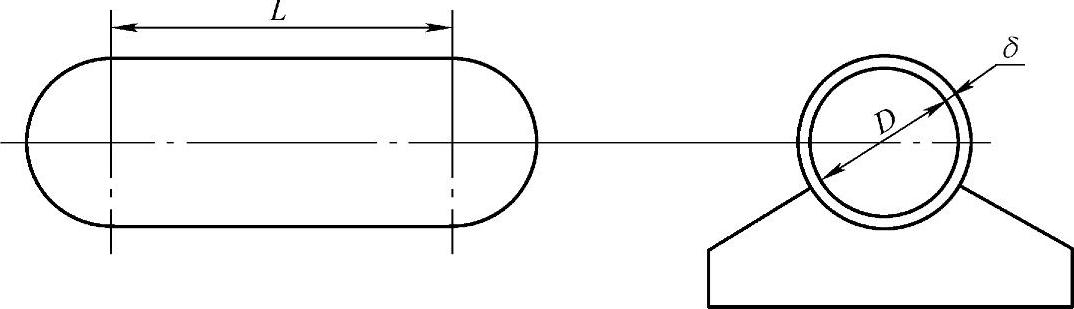
图8-1 卧式储罐示意图

已知条件：容积V=2×10⁶cm²，材料密度ρ=0.01kg/cm³，介质内压p=10MPa，[σ]=200MPa。

1.设计变量

取直径和厚度为独立的设计变量，其取值范围为大于零的实数，记为

X=[x₁，x₂]^T=[D，δ]^TX∈E² （8-8）

2.目标函数

以质量最小为优化目标，即

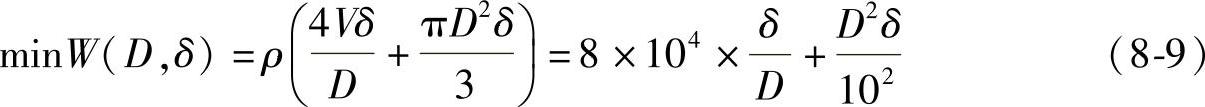
于是得目标函数为

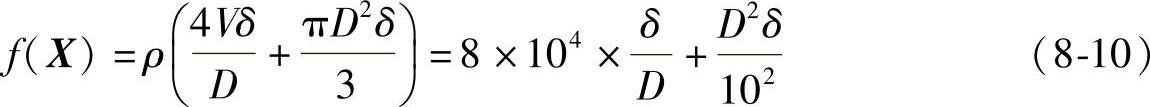
3.约束条件

（1）壁厚条件 壁厚δ上限δ″=6cm，下限δ′=0.4cm。尺寸约束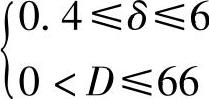：，由此得

g₁（X）=0.4-δ≤0

g₂（X）=δ-6≤0 （8-11）

（2）强度条件 容器容积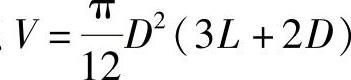，则长度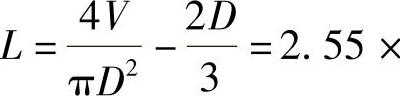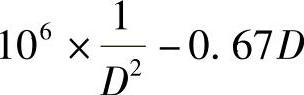，约束条件L≥8D，即解得0＜D≤66cm。容器表面积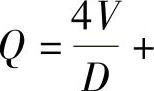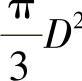，跨距中点处最大轴向应力约束：

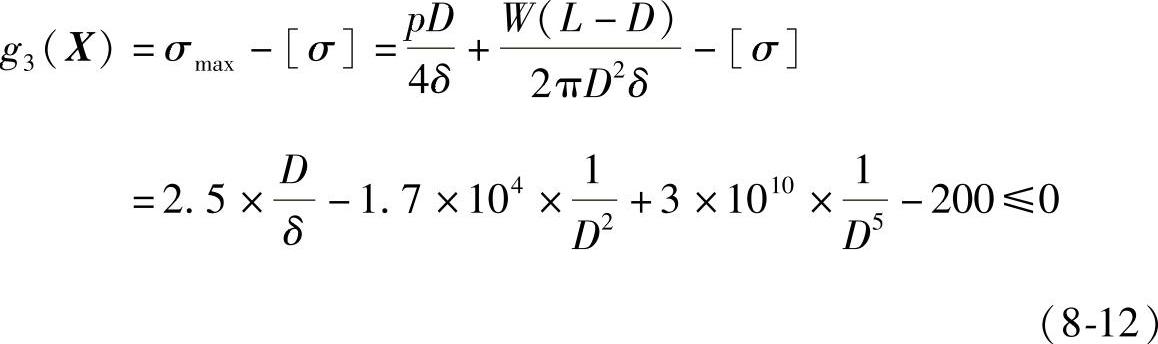(www.daowen.com)

4.优化方法

构造库恩-图克函数K（D，δ）=W（D，δ）+λh（D，δ），并根据库恩-图克极值条件进行寻优。

由式（8-4）得

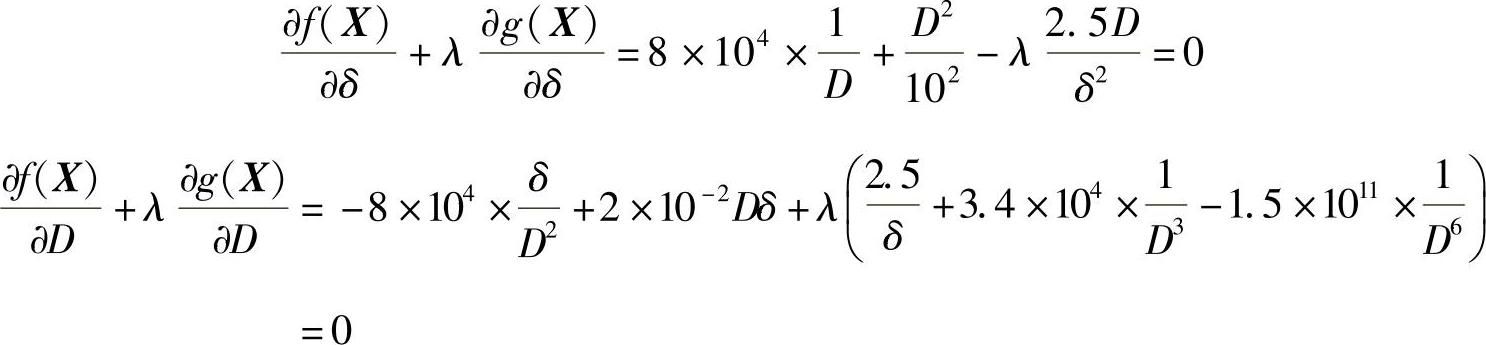
由式（8-5）得

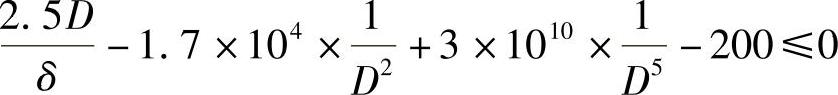
由式（8-6）得

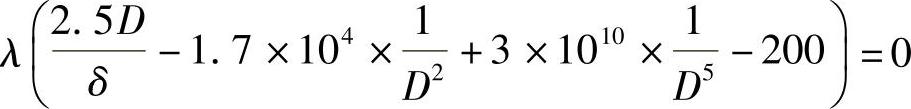
由式（8-7）得

λ≥0

5.分析与讨论

若λ=0，则由式（8-4）知D^*=-200＜0，不符合原题约束条件，故不成立。

若λ＞0，则由式（8-4）、式（8-6）可得D^*=61cm，δ^*=0.77cm，λ^*=0.52（因属非线性方程组求解，其步骤较繁，这里从略）。因其解全部满足极值条件，故最优化解应为：D^*=61cm，L^*=644cm，δ^*=0.77cm，容器质量W（D^*，δ^*）=1038.5kg。

现将上、下两组相邻参数的计算结果，列于表8-1。

表8-1 三组储罐数据对照

由表8-1可知，在其最大应力不超过许用应力，且满足约束条件，最优解计算出的质量是最轻的。为了不使计算太过复杂、烦琐，本节中只举2m³的储罐。由对照可知，求最优解可节省十几公斤的材料。现在的大型储罐都是几百立方米的。若按最优化解，每一个储罐都可节省数吨至十几吨的材料。因而可大大降低成本，取得较大的经济效益。因此，对非线性规划有约束条件的设计可运用此法进行优化计算，可使设备在足够强度条件下，有显著的经济效益。