在实际设计容器时,常常以最小质量或最低成本进行优化设计,它和最小表面积问题的差别在于必须考虑材料强度、壳体壁厚、容许应变以及压力、温度等因素。对于受一定内压的容器设计,要求具有最小质量或最低成本的设计,可归结为具有最小表面积的纯几何问题。
已知一簿壁细长不锈钢容器的壁厚不小于Smin=0.25mm,为保持密封、防漏,壳体径向挠度δmin=0.025mm,容器内压力为p=16.8MPa,许用应力[σ]=400MPa,弹性模量E=2×105MPa,泊松比μ=0.33。试设计使其壳体单位体积质量为最少。
1.设计变量
若筒体长度一定,则可取筒体直径和壁厚为设计变量,即
X=(x1,x2)T=(D,δ)T (7-45)
式中 D——直径(mm);
δ——壁厚(mm)。
2.目标函数
对于细长圆筒,其底部质量可忽略。这样,若以最小质量(或最低成本)优化设计目标,则目标函数可表达为
f(X)=minf(D,δ)=πDLδρ/(πD2L/4) (7-46)
3.约束条件
(1)径厚比条件 对于细长圆筒,直径与壁厚比值大于20(即D/δ≥20),于是有
g1(X)=20δ-D≤0 (7-47)
(2)最小壁厚条件 一般地,要求δmin=0.25mm,故
g2(X)=0.25-δ≤0 (7-48)
(3)强度条件 压力容器工作时,其强度须满足强度条件:σ≤[σ]。由第4强度理论知:
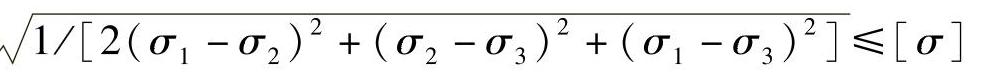
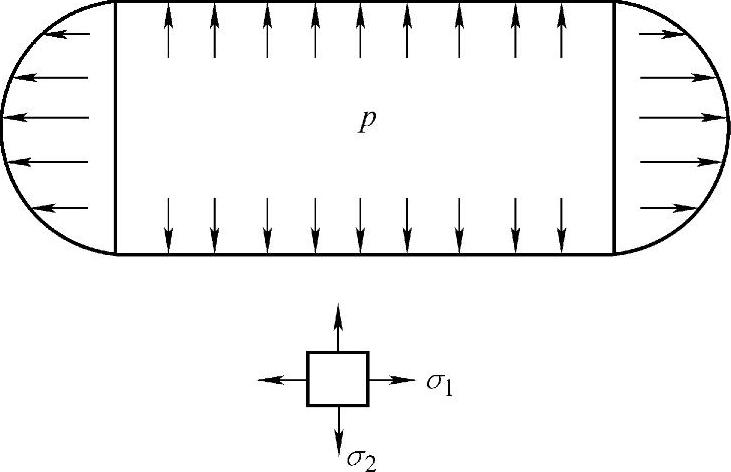
薄壁圆筒受力如图7-5所示,只存在二向应力: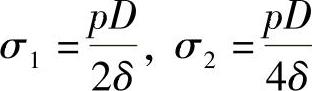
 (www.daowen.com)
(www.daowen.com)
图7-5 薄壁圆筒受力示意图
于是
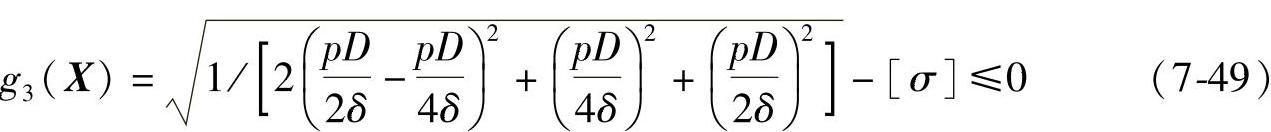
或
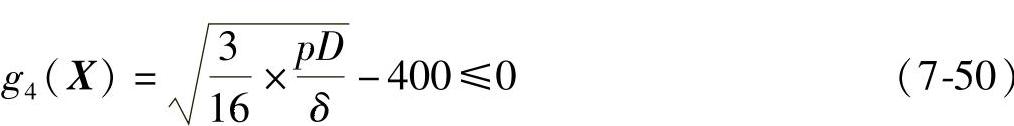
(4)径向挠度条件 由簿壁容器有力距理论知,容器受内压,引起弯曲变形,径向产生位移:
ζ=εtR
而 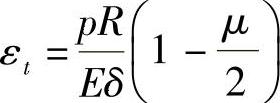
所以 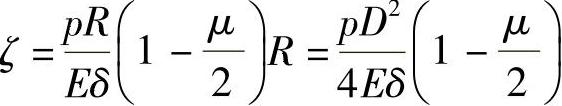
式中 εt——周向应变;
R——半径(mm)。
要求容器弯曲变形应小于最小弯曲变形ζmin,即
ζ≤ζmin
又
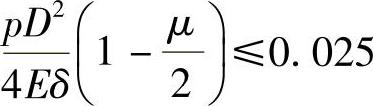
所以
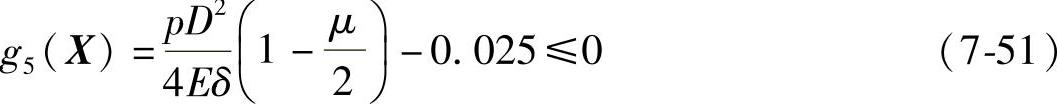
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







