1.设计变量

如前所述，压力容器壳体质量是由内径D_i、筒体长度L及壁厚δ_n确定的，在设计参数一定的情况下，由D_i、L便可确定壳体壁厚δ_n，因此按照上述优化的基本思想、选择壳体的形状参数D_i、L作为设计变量（图7-2）。即

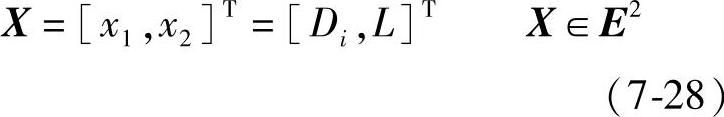
2.目标函数

优化设计的目的就是要在安装空间允许的情况下，寻找壳体质量较小的相应壳体尺寸，即其目标函数就是壳体质量minM（D_i，L），其表达式按壳体的展开形状确定。

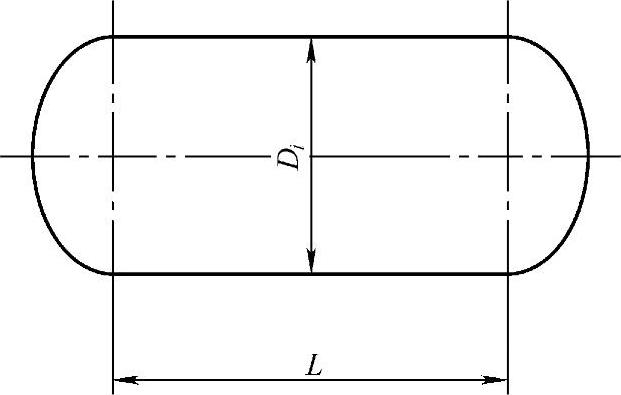
图7-2 卧式容器简图

（1）筒体质量 筒体为可展开零件，其展开形状为长度为L，宽度为πD_m的矩形板材，该板材的厚度为筒体的厚度δ₁，故其质量表达式为

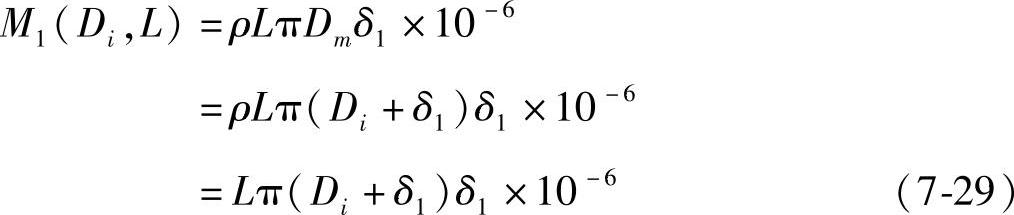
式中 ρ——材料密度（kg/m³），取ρ=7.85×10³kg/m³；

L——筒体长度（mm），包括封头直边长度；

D_m——筒体中径（mm），D_m=D_i+δ₁；

D_i——筒体内径（mm）；

δ₁——筒体壁厚（mm）。

（2）封头质量 椭圆封头为不可展开零件，按等面积法展开，即假设封头中性层曲面的面积与其展开面积相等。该展开图为圆，其直径为

D=（1.38D_m+4D_mh）^1/2

式中 D_m——封头中性层直径（mm），D_m=D_i+δ₂；

D_i——封头内径（mm）；

δ₂——封头壁厚（mm）；

h——封头直边高度（mm）。

考虑到封头直边高度质量已经计入筒体部分，在此封头质量只考虑椭圆曲线部分，即h=0时展开形状（圆形板料）的质量，该展开图的直径D为1.175D_m，厚度为封头名义厚度δ₂，故两个封头质量M₂（D_i，δ₂）表达式为

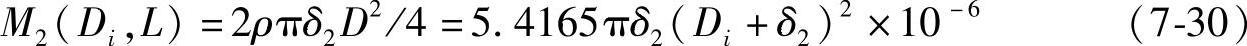
总的目标函数M（D_i，L）即为式（7-29）与式（7-30）之和：

3.约束条件函数

（1）全容积约束条件 由D_i、L所确定的壳体全容积必须满足用户要求的值VN。

由相关资料可知，双标准椭圆封头圆筒形容器全容积公式为

VN=πD³_i/12+πLD²_i/4

由此有约束方程式：

（2）几何约束条件 令式（7-32）中L=0，得到D_i=D_JX=（12VN/π）1/3，这是一个极限情况。根据相关资料，椭圆封头的最大内径D_i=5200mm，为了使封头内径既不超过这个范围，又满足全容积值VN，令D_i≤G_JX，且D_i≤5200。

于是有约束方程式：

（3）强度条件根据GB150—1998《铜制压力容器》的规定，壳体厚度必须满足相应的厚度计算公式。

筒体：S_j1=pD_i/（2[σ]^tφ-p）+C₂

S_j1加上钢板厚度负偏差C₁后向上圆整至钢板厚度即得筒体厚度δ₁。

封头：S_j2=pD_i/（2[σ]^tφ-0.5p）+C₂

S_j2加上钢板厚度负偏差C₁后向上圆整至钢板厚度即得封头厚度δ₂。

式中 S_j1——筒体设计厚度（mm）；(www.daowen.com)

S_j2——封头设计厚度（mm）；

[σ]^t——设计温度下筒体或封头材料的许用应力（MPa）；

φ——焊缝成形系数；

C₂——腐蚀裕量（mm）。

为了满足以上条件，得到约束方程：

然后加上钢板厚度负偏差C₁通过计算机自动向上圆整至钢板厚度得到筒体厚度δ₁和封头厚度δ₂。

（4）最小厚度条件为了满足制造工艺要求及运输和安装过程中刚度要求，按GB150—1998（《钢制压力容器》），以及根据工程实践经验，对壳体规定了不包括腐蚀裕量C₂的最小厚度要求。

碳素钢和低合金钢筒体：

当D_i≤3800mm时，δ₁≥2D_i/1000，且δ₁≥30mm；

g₆（X）=δ₁-2D_i/1000≥0 （7-35）

g₇（X）=δ₁-3≥0 （7-36）

当D_i≥3800mm时，按实际情况确定。

不锈钢筒体δ₁≥2mm。所以有

g₈（X）=δ₁-2≥0 （7-37）

封头：受内压标准椭圆封头的有效厚度δ_e应不小于封头内径D_i的0.15%，由此得到约束方程：

g₉（X）=δ₂-C₂-C₁-0.15%D_i≥0 （7-38）

（5）压力试验条件 压力试验一般采用液压试验，对不适合作液压试验的容器，可以采用气压试验。

由GB150—1998（《钢制压力容器》），得到液压试验压力p_T：

p_T=1.25p[σ]/[σ]^t或0.1+p的较大值。

液柱静压力p_T=Hρ×0.0000098MPa

液压试验时，筒体的薄膜应力σ_T须满足如下条件：

σ_T=（p_T+p₁）（D_i+δ_e）/2δ_eφ≤90%σ_s

上述式中 [σ]——试验温度下材料的许用应力（MPa）；

[σ]^t——设计温度下材料的许用应力（MPa）；

p——压力容器的设计压力（MPa）；

ρ——液体密度（g/cm³）；

δ_e——筒体有效厚度（mm），δ_e=δ₁-C₁-C₂；

σ_s——试验温度下材料屈服点（MPa）；

D_i——筒体内径（mm）；

H——液柱高度（mm），其中卧式容器：H=D_i+400+2δ₁；立式容器：H=L+D_i/2-f+400+2δ₂，其中“400”系假定上下接管伸出高度均为200mm时在液柱高度立的增加值，这样考虑一般与实际设计中的接管伸出高度是一致的；

L——筒体长度（包括封头直边高度）（mm）。

于是得到约束方程：

g₉（X）=0.9σ_s-（p_T+p₁）（D_i+δ_e）/2δ_eφ≥0 （7-39）

对气压试验，试验压力p_T=1.15p[σ]/[σ]^t或0.1+p中的较大值。筒体薄膜应力须满足如下条件：

σ_T=p_T（D_i+δ_e）/2δ_eφ≤80%σ_s

此时约束方程为

g₁₀（X）=0.8σ_s-p_T（D_i+δ_e）/2δ_eφ≥0 （7-40）