对于一般P（＞2）个目标的情况，完全与上述归纳的步骤类似。先求P个单目标规划问题（P₁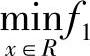）（X）的最优解，设为x¹，j=1，2，…，P。记作f²₁=f₁（x¹），i=1，2，…，p，j=1，2，…，p。过P个点[f¹₁，f₂¹，…，f_p¹，i=1，2，…，p]。做超平面，设其方程为

式（6-50）是一个具有（P+1）个变量h₁，h₂，…，β的（P+1）个方程的线性方程组，由此可确定一组解来作为权系数。

为了便于设计者求解，本节根据列主元高斯消去法，用FORTRAN语言编写了求解式（6-50）的计算程序。

1.使用说明

（1）子程序语句 SUBR0UTINE GS（A，N，M，EPS）

（2）哑元说明 输入参数：

N整变量，方程组的阶数

M整变量，M=N+1

EPS实变量，消元过程中主元的最小允许值，如果主元小于此值，则停机，打印STOP4444。

输入兼输出参数：

A N*M个元素的二维实效组。开始存放方程组的系数与右端项组成的增广矩阵。最后在第M列存放方程组的解。

2.程序

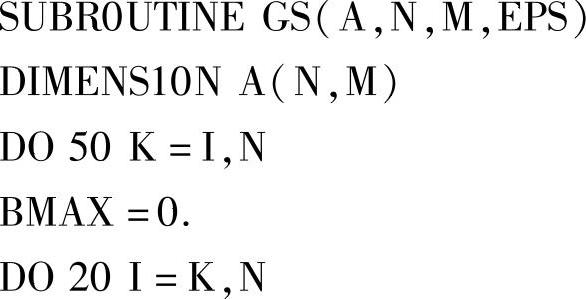
3.实例

当求解双目标及多目标问题时，都可以利用上述程序求出权系数。

【例6-2】 某动压滑动轴承设计主要参数为：径向载荷F=18000N，d=100mm，转速n=5000r/min。要求用油量最少（f₁），温升最低（f₂）。表6-1为f₁、f₂的单目标最优点上，两目标函数f₁、f₂的函数值。欲用线性加权法求解（VP）问题，求出权系数λ₁、λ₂。(www.daowen.com)

表6-1 单目标最优点上f₁、f₂的函数值

解 已知f¹₁=9.8032，f²₁=30.0021，f₂¹=968.5905，f²₂=0.2361代入式（6-50）：λ₁f¹₁+λ₂f₂¹=β

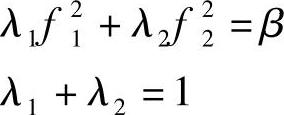
将方程组写为矩阵形式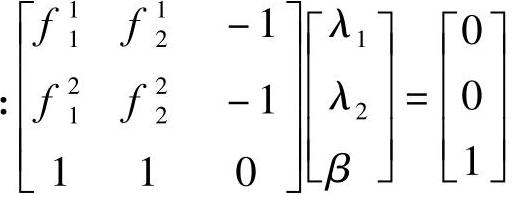

令x₁、x₂、x₃分别等于λ₁、λ₂、β。

取N=3，M=4，EPS=10^-9数组A表示增广矩阵。

程序如下：

SUBROUTIEGS（A，N，M，EPS）

{本子程序段段部分

输入数据与计算结果见表6-2、表6-3。

表6-2 数据

表6-3 计算结果