评价函数法是处理多目标优化问题时常用的实用方法。其基本思想是人为地构造一个新的函数——通常称为评价函数，从而将多目标优化问题转变为求该评价函数的单目标优化问题。按照不同的想法构造不同的评价函数，就得到不同的评价函数法，其中线性加权法是最常用且最重要的一种方法。

多目标优化问题的数学模型一般表达式为

或记作

其中Ω⊆Eⁿ，将f₁（X），f₂（X），…，f_p（X）视为向量目标函数f（X）的分量，可表示为

所谓线性加权法就是先对各个单目标函数f₁（X），f₂（X），…，f_P（X）按其重要程度，对应地给出一组系数λ₁，λ₂，…，λ_P并有

取f₁（X）与λ₁（i=1，2，…，P）的线性组合为评价函数，即：(www.daowen.com)

再求单目标问题：

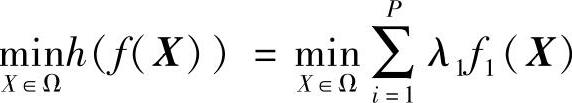的最优解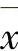，即为多目标优化问题式（6-45）的最终解答。

借助评价函数h（f）把多目标优化问题转化为求单目标问题的最优解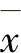，至于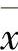是否为多目标问题的有效解或弱有效解，是人们所关心的。若评价函数的最优解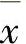不是多目标问题的有效解或弱有效解，则毫无意义。

可以证明：当人为构造的评价函数是严格单调增函数时，则单目标问题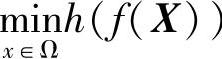的最优解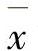为多目标规划问题式（6-45）的有效解；若h（f）是单调增函数时，则单目标问题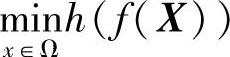的最优解为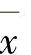为多目标问题式（6-45）的弱有效解，至于线性加权法。当权系数均大于零时，评价函数h（f）为f的严格单调增函数；当权系数中有等于零者时，h（f）为f的单调增函数。故该评价函数的最优解就是多目标优化问题式（6-45）的有效解或弱有效解。