一般的优化设计方法只能求得连续变量的最优解，但是在机械设计中常遇到一种混合设计变量的问题，即在数学模型中同时存在连续、整型和离散型设计变量。随着标准化、规格化程度的不断提高，某些机械产品的设计变量只能取离散或整型值的情况日益普遍化。因此，发展离散变量优化设计方法就成为目前机械优化设计发展中的一个重要的方向。

常用的混合离散变量的优化方法有凑整解法、网格法、离散变量的随机试验法、自适应随机搜索法、组合形法、离散性惩罚函数法等。限于篇幅，本节仅简要介绍前两种方法。

1.凑整解法

目前，解决混合离散变量问题的最常用方法是凑整解法。其基本思想是，先权宜地视所有变量为连续变量，在求得连续最优解后，再把它的各分量舍入到与其最接近的整数值或离散值上。采用凑整解法来处理混合离散设计变量问题，只允许向可行域内调整。应该注意到，当约束函数为严重非线性，而且约束区域为一个非凸集时，采用该法有可能得不到一个可行设计方案。

2.网格法

网格法的基本思想是：在离散设计变量的值域（离散空间）内，按离散点依次取点，检查离散点X是否可行；若可行，即计算它的目标函数值f（X），并与前面计算所取得的最好点的目标函数值相比较，若f（X）比它小（对于求目标函数的极小化情况），则存储当前所取得的最好离散点解；否则再计算其他离散点。当全部可行点都查过一遍时，其最好点即为问题的约束离散最优解（图6-3），故又称为枚举法。(www.daowen.com)

二维优化设计问题网格法的程序框图如图6-4所示。

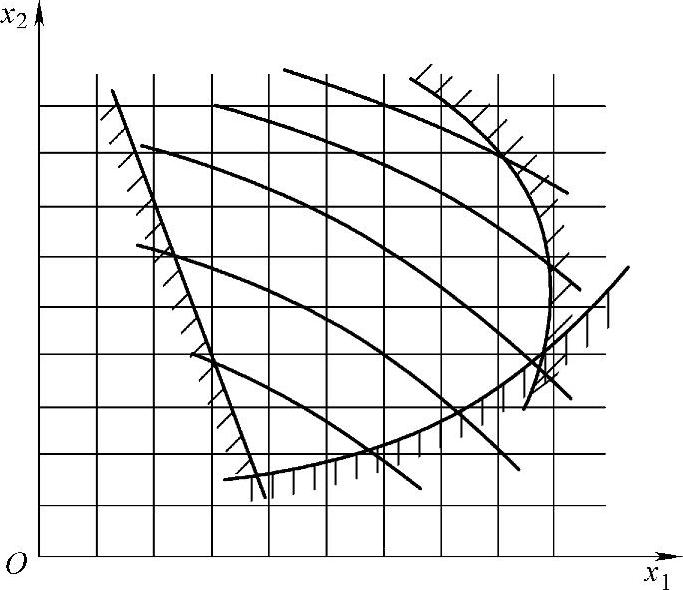
图6-3 网格法示意图

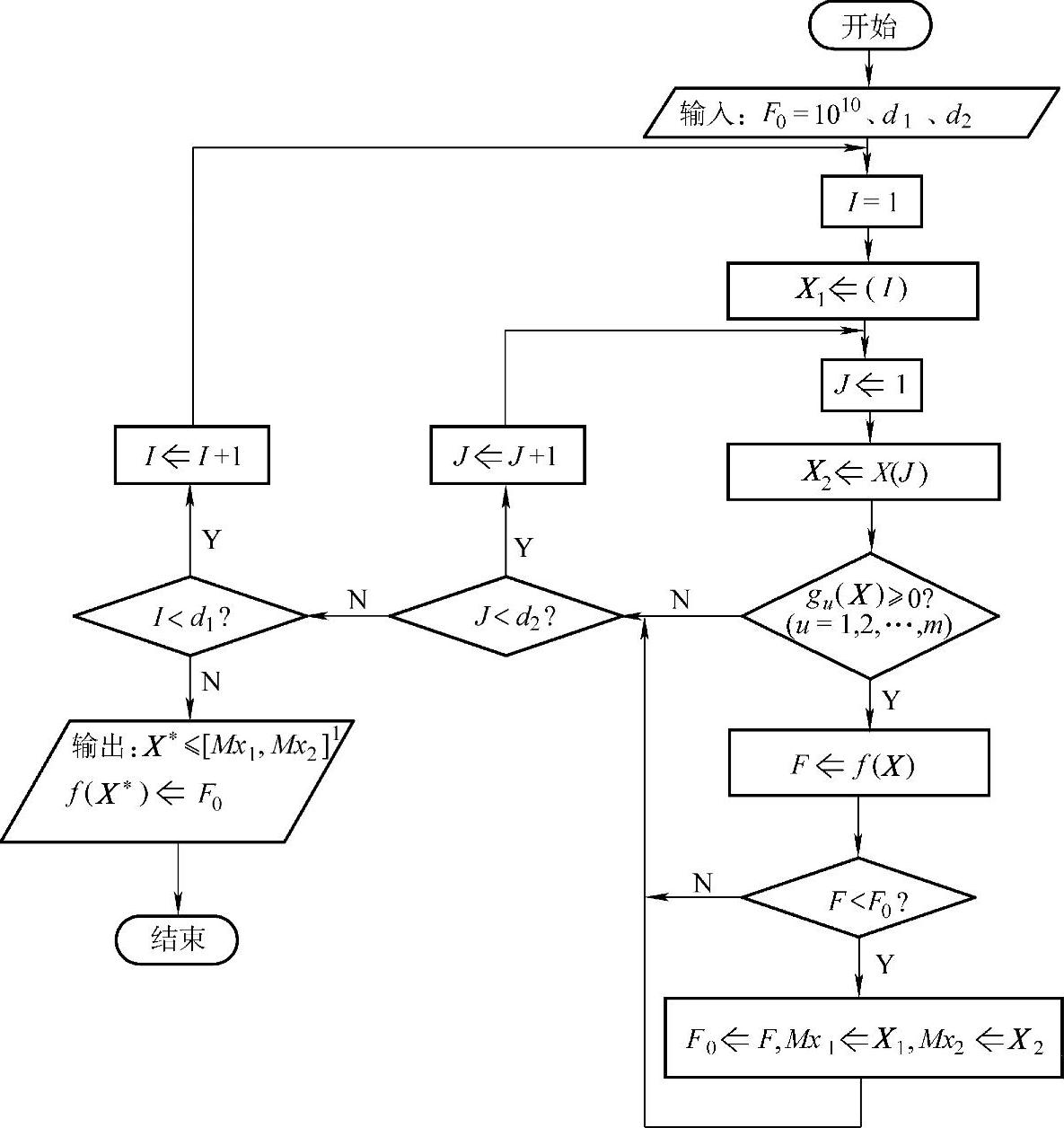
图6-4 二维优化设计问题网格法的程序框图