在第1章中，曾介绍过优化设计数学模型的基本概念，它包括目标函数和约束条件，是关于优化设计问题的数学表达形式，反映了设计问题中各主要因素间内在联系的一种数学关系。因此，正确地建立一个数学模型，乃是解决优化设计问题的关键。

1.建立数学模型的基本条件

建立一个正确的压力容器优化设计数学模型通常要求满足如下两个基本条件：

1）数学模型能在特定的条件下准确地、可靠地说明设计问题所要达到的目的、所受的限制条件，以及能预测设计方案的变化，估计结果的可靠性等。

2）数学模型要容易处理，即计算过程要简化并易于实现。

如果数学模型过于复杂，尽管能正确地表达设计问题，但不便于处理和计算，从而限制了它的应用；反之，则不一定能全面而准确地描述设计问题。这常常是一对矛盾。要解决好这对矛盾，设计者除了能抓住设计问题的要点。运用现代科学理论建立表达式，并且具有识别和处理复杂数学模型的能力之外，还需要按正确的步骤和方法进行。

2.建立数学模型的步骤与方法

1）首先，对设计问题加以认真的研究并抓住其本质特征，了解常规所用的设计方法，然后研究选用适当的数学、物理和力学的方法。

2）选择与设计问题本质有关的，对结果影响最重要的因素，确定设计变量并构造初步的数学模型。

3）将初步的数学模型和设计问题加以比较，若不能精确表达设计问题时，则用逐步逼近的方式修正模型。

4）若数学模型复杂，需要采用近似数值计算方法，则应能对其误差值有一正确的估计。

3.设计变量和约束条件的确定

（1）设计变量 建立数学模型的第一步是要确定哪些参数为设计变量，哪些参数取为常量。从理论上说，任何一种参数都可按设计变量处理，但这样一来，数学模型变得相当复杂。这在实际上不一定合理，甚至是不可能的。因此，应尽量加以甄别，以减小模型的维数。例如，对于材料的物理力学性能，常常需要用试验方法来确定，所以用赋值的方法按常量处理较为合理。而在设计中常遇到的一些因变量，如应力、应变、挠度、压力、温度、功率等，它们都具有一定的函数关系式，若这种参数在数学上易于消去，则一般不把其定为设计变量。反之，则也可取为设计变量，列出相应状态方程（等式约束函数），并将设计变量分为决策变量和状态变量。

（2）约束条件 在优化设计中，对于一个性能指标，既可取为目标函数，亦可定为设计约束，即两者是可以相互置换的。在确定设计约束时，一般可以比常规设计考虑更多方面的要求，如工艺、装配、费用、性能要求等。只要某种限制能够用设计变量表示为约束函数（包括经验表达式、近似表达式），都可以确定为约束条件。

当一个约束条件不仅依赖于设计变量，而且还与另外一种参数有关时，则称为参数约束。例如，对于桥式起重机桥架的优化设计，由于小车是沿桥架移动的，所以桥架内的工作应力是载荷位置X的函数，其不等式约束条件为

g（X）=σ（X）-[σ]≤0

此外，在化工原料合成过程中，容器壳体强度既是压力的函数，又是温度的函数。若对强度加以限制，则所建立的约束是压力和温度参数的约束。因而，在压力容器优化设计中，对于参数约束条件，必须保证它在参数的变化范围内均能满足。

在数学模型中，当有的设计变量仅在约束条件中出现，而在目标函数中不包含它时，应仔细检查计算公式，弄清该设计变量的允许取值范围，以便建立一个补充约束条件。若要求该变量的最优值，则可在优化设计结束时转入第二次优化设计，即将其原目标函数用其最优值建立一个约束条件，而将与该参数有关的约束函数建立目标函数，然后求极小化。采用这种方法，要求在程序设计时，目标函数和约束函数容易隔离和置换。

【例6-1】 图6-2所示为卧式压力容器结构简图。设压力容器壳体壁厚δ_n已确定，试按前述的优化设计基本思想，建立其优化设计的数学模型。

1.目标函数

本优化设计的目标就是要在安装空间允许的情况下，寻找壳体质量最小的相应壳体尺寸，即目标函数是壳体质量M（D_i，L）最小，其表达式按壳体的展开形状确定。

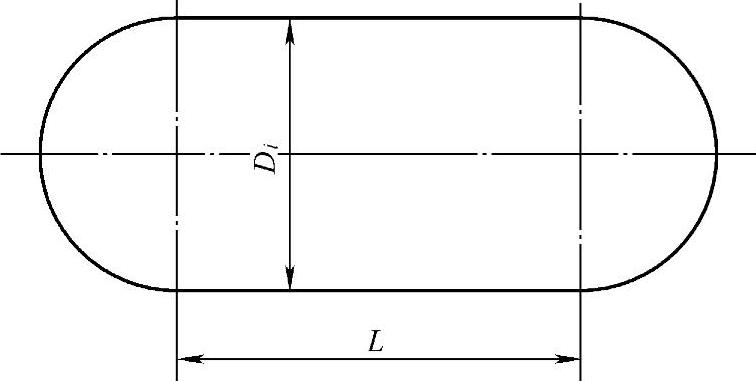
图6-2 卧式压力容器简图

（1）筒体质量 筒体（圆筒）为可展开零件，其展开形状为长度为L，宽度为πD_m的矩形板材，该板材的厚度为筒体的厚度δ₁，故其质量表达式为

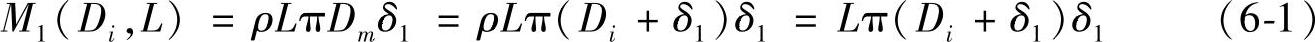
式中 ρ——材料密度（kg/m³），取ρ=7.85×10³ kg/m³；

L——筒体长度（mm），包括封头直边长度；

D_m——筒体中径（mm），D_m=D_i+δ₁；

D_i——筒体内径（mm）；

δ₁——筒体壁厚（mm）。

（2）封头质量 椭圆封头为不可展开零件。若按等面积法展开，即假设封头中性层曲面的面积与其展开面积相等，则可得到展开图形为圆，其直径为

D=（1.38D_m+4D_mh）^1/2 （6-2）

式中 D_m——封头中性层直径（mm），D_m=D_i+δ₂；

D_i——封头内径（mm）；

δ₂——封头壁厚（mm）；

h——封头直边高度（mm）。

考虑到封头直边高度质量已经计入筒体部分，在此封头质量只考虑椭圆曲线部分，即h=0时展开形状（圆形板料）的质量，该展开图的直径D为1.175D_m，厚度为封头名义厚度δ₂，故两个封头质量M₂（D_i，δ₂）表达式为

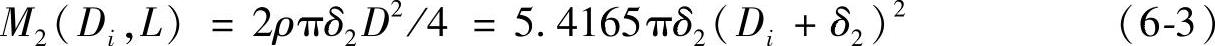
由式（6-1）和式（6-3），可得壳体总的质量为

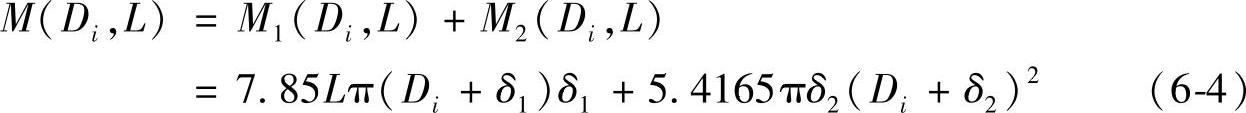
于是，本优化设计的目标函数为

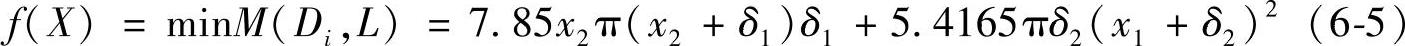
2.设计变量

综上所述，壳体总质量主要取决于内径D_i和筒体长度L，故为取设计变量。即

3.约束条件

（1）全容积VN由D_i、L所确定的壳体全容积必须满足用户要求的值VN。

对于双标准椭圆封头圆筒形容器，全容积公式为

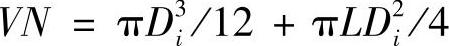(www.daowen.com)

由此有约束方程式：

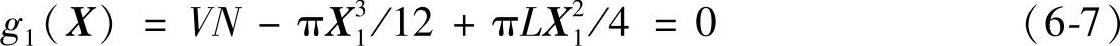
（2）优化范围的最大上限值D_max上式中令L=0，得到D_i=D_JX=（12VN/π）1/3，这是一个极限情况。根据旋压封头相关标准，椭圆封头的最大内径D_i=5200mm，为了使封头内径既不超过这个范围，又满足全容积值VN，令D_i≤G_JX，且D_i≤5200。

于是有约束方程式：

g₂（X）=D_JX-x₁≥0

g₃（X）=5200-x₁≥0 （6-8）

（3）强度条件 根据GB 150—1998《钢制压力容器》的规定，壳体厚度必须满足相应的厚度计算公式。

圆筒设计厚度S_j1加上钢板厚度负偏差C₁后，通过计算机自动向上圆整至钢板厚度即得筒体厚度δ₁。而

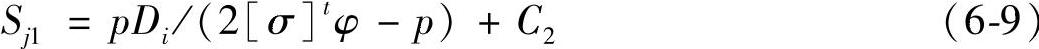
类似地，封头设计厚度S_j2加上钢板厚度负偏差C₁后，通过计算机自动向上圆整至钢板厚度即得封头厚度δ₂。而

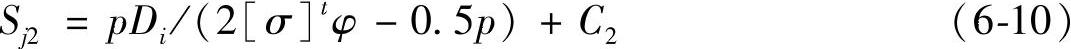
式中 [σ]^t——设计温度下筒体或封头材料的许用应力（MPa）；

φ——焊缝成形系数；

C₂——腐蚀裕量（mm）。

为了满足以上条件，得到约束方程：

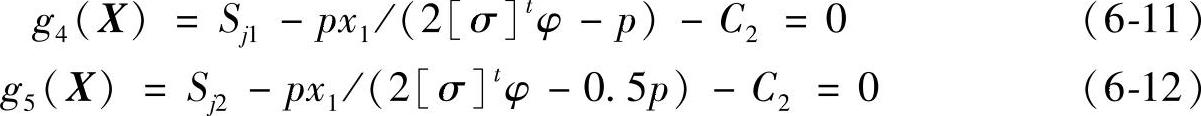
（4）最小厚度条件 为了满足制造工艺要求及运输和安装过程中刚度的要求，据工程实践经验，对壳体规定了不包括腐蚀裕量C₂的最小厚度要求。

对于碳素钢和低合金钢筒体，当D_i≤3800mm时，δ₁≥2D_i/1000，且δ₁≥30mm，于是

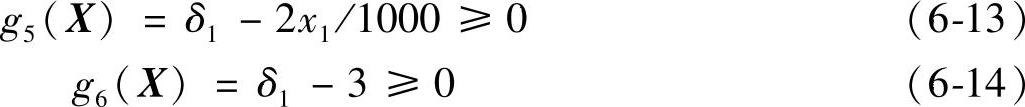
当D_i≥3800mm时，按实际情况确定。

对于不锈钢筒体，δ₁≥2mm。所以有

g₇（X）=δ₁-2≥0 （6-15）

对于受内压标准椭圆封头，其有效厚度δ_e应不小于封头内径D_i的0.15%，由此得到约束方程：

g₈（X）=δ₂-C₂-C₁-0.15%x₁≥0 （6-16）

（5）压力试验条件 压力试验一般采用液压试验。对不适合作液压试验的容器，可以采用气压试验。

1）液压试验压力：

p_T=1.25p[σ]/[σ]^t或0.1+p的较大值

2）液柱静压力：

p_T=Hρ×0.0000098

液压试验时，圆筒的薄膜应力σ_T须满足如下条件：

σ_T =（p_T+p₁）（D_i+δ_e）/2δ_eφ≤90%σ_s

式中 [σ]——试验温度下材料的许用应力（MPa）；

[σ]^t——设计温度下材料的许用应力（MPa）；

p——压力容器的设计压力（MPa）；

ρ——液体密度（g/cm³）；

δ_e——圆筒有效厚度（mm），δ_e=δ₁-C₁-C₂；

σ_s——试验温度下材料屈服点（MPa）；

H——液柱高度（mm），其中卧式容器：H=D_i+400+2δ₁，立式容器：H=L+D_i/2-f+400+2δ₂；

L——立式容器的筒体长度（mm）（包括上下封头的直边高度）；

D_i——筒体内径（mm）。于是得到约束方程：

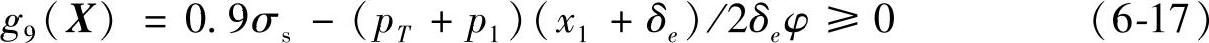
3）气压试验压力：

p_T =1.15p[σ]/[σ]^t 或0.1+p中的较大值

圆筒薄膜应力须满足如下条件：

σ_T=p_T（D_i+δ_e）/2δ_eφ≤80%σ_s

此时约束方程为

g₁₀（X）=0.8σ_s-p_T（x₁+δ_e）/2δ_eφ≥0 （6-18）

这是一个二维的约束非线性规划问题。