与内点法将惩罚函数定义于可行域内，且求解无约束问题的探索点总是保持在可行域内的特点不同，外点法的特点是将惩罚函数定义于约束可行域之外，且求解无约束问题的探索点是从可行域外部逼近原目标函数的约束最优解的，它既可处理带不等式约束的问题，又能求解含等式约束的问题。

外点惩罚函数法构造的新的目标函数的一般形式随约束条件的不同而异。

1）当约束条件为g_u（X）≤0（u=1，2，…，m）时：

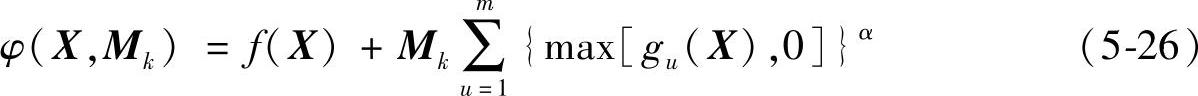
式中 α——构造惩罚函数的指数，其值将影响φ（X，M_k）等值线在约束面处的性质，一般取α=2；

M_k——惩罚因子，是大于零的一个递增数列，即应满足：0＜M₀＜M₁＜M2＜…＜M_k＜…，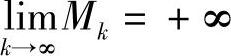

在惩罚项中：

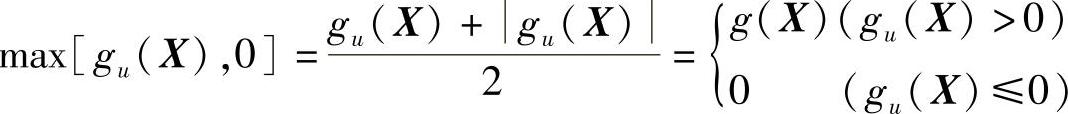
2）当约束条件为g_u（X）≥0（u=1，2，…，m）时：

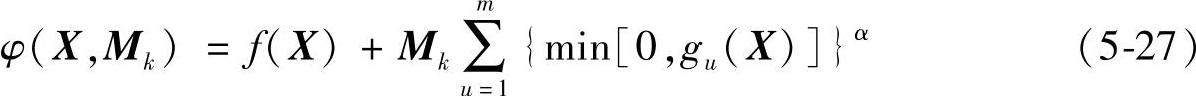
一般取α=2。同样应满足：

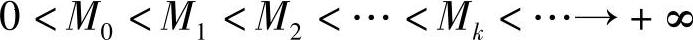
而在惩罚项中：

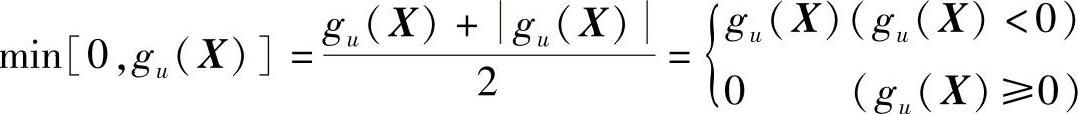
3）当约束条件中尚包括h_v（X）=0（v=1，2，…，p）的等式约束时，则在式（5-26）、式（5-27）中的右边加进。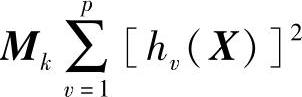

容易看出，上述两式中的惩罚项在可行域内部点上其值为零。惩罚因子M_k被取成递增正数序列，以不断强化惩罚项作用，把φ（X，M_k）的最小点逐步引向约束最优点X^*。在此过程中，惩罚项之值将逐渐减小，直至为零（到达约束面上）为止，因此它又称为衰减函数。

外点惩罚函数法的计算步骤如下：(www.daowen.com)

1）选择一个初始点X^（0），并选择适当的M₀＞0，给定允许误差ε₁＞0和ε₂＞0，确定递增系数，令k=k+1。

2）以X^（k-1）为起点，用无约束最优化算法求φ（X，M_k）的最小点X^（k）=X^*（M_k）。

3）检查X^（k）-X^（k-1）≤ε₁及f（X^（k））-f（X^（k-1））≤ε₂。

4）如果满足3）中收敛准则，终止计算，取X^*=X^（k）；否则，取M_k+1=CM_k，其中，可取递增系数C=8，然后，可令k=k+1，返回到2）。

【例5-7】试用外点惩罚函数法求目标函数f（X）=x₁+x₂在约束条件g₁（X）=-x²₁+x₂≥0，g₂（X）=x₁≥0下的最优解。

解 构造惩罚函数：

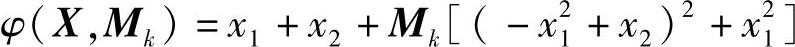
为说明问题，用解析法求解：

解此方程组，得

…

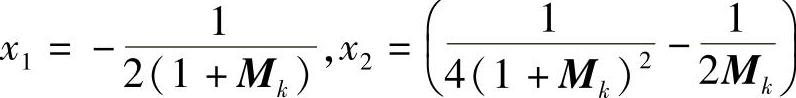
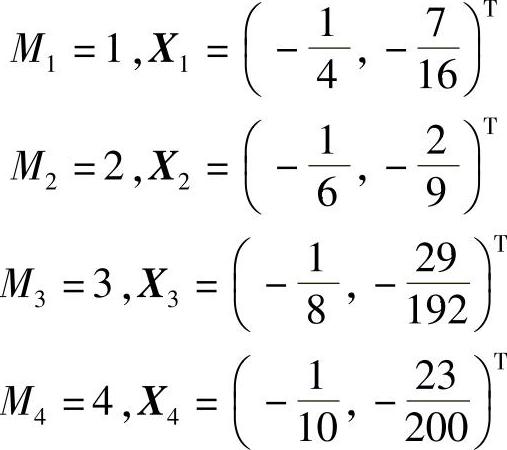
M_k→∞，X_k=（0，0）^T

图5-9表示目标函数等值线与可行域的关系。从图中看出，X_k从可行域的内部随着M_k的增大而收敛于原问题的最优解X^*=（0，0）T。