内点惩罚函数法仅适用于具有不等式约束的优化问题,根据下列的目标函数和约束条件函数:
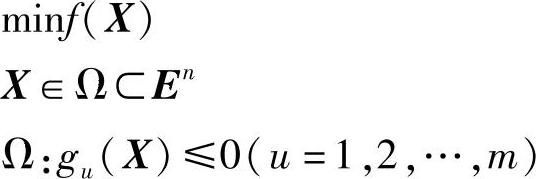
构造新目标函数φ(X,rk)的无约束优化问题:
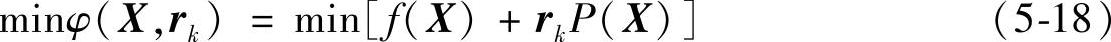
式中 rkP(X)——障碍项;
P(X)——依赖于gu(X)的障碍函数;
rk——惩罚因子,它满足:①r0>r1>r2>…;②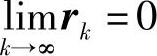 。
。
P(X)的取法使得当设计点X在区域内部且离边界很远时,其值几乎为零,φ→f;而当X从内部靠近边界时,P(X)→∞。P(X)的作用相当于在原约束的边界上筑起一道屏障,防止设计点越出可行域,所以内点惩罚函数法又称障碍函数法。由前可知,最优解往往是在边界上,为了允许设计点逐渐接近边界,随k→∞,让rk→0,使得对设计点靠近边界所受的惩罚逐渐减小。
最常见的惩罚函数P(X)及因子rk的取法为
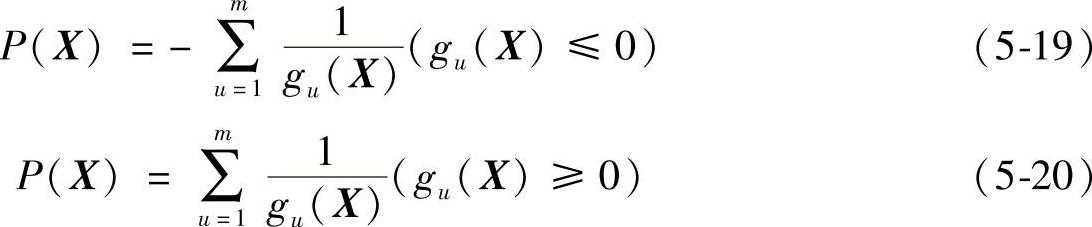
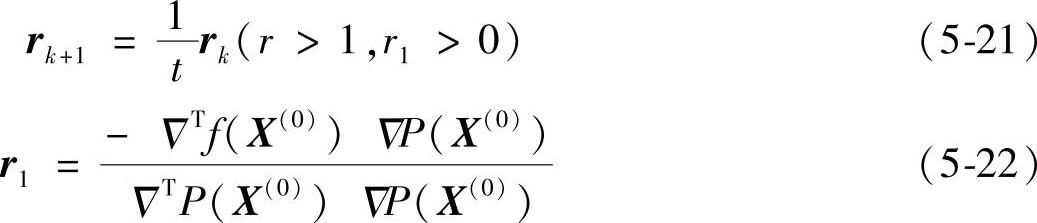
式中 t——给定常数。
内点惩罚函数法求约束优化问题的算法如下:
1)选取一个初始可行设计点X(0)和适当的r1及t,令k=1。
2)从X(k-1)出发优化φ(X,rk),记为X*=X(k)。
3)检查收敛准则:
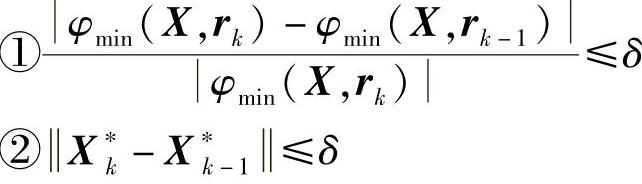
如满足则停止;否则进行4)。
4)计算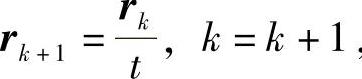 ,返回2)。(https://www.daowen.com)
,返回2)。(https://www.daowen.com)
【例5-6】 利用内点惩罚函数法求解目标函数f(X)=x-1,约束条件为x≥0的最优解。
解 构造内点惩罚函数:
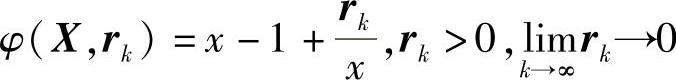
对于固定的rk,φ(X,rk)的极小点满足:
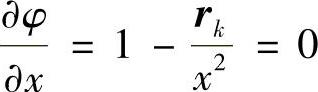
解得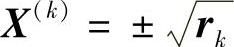
为保证X(k)的可行性,应取正根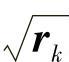 。显然,当k→∞时,rk→0,X(k)→0。事实上,X*=0也就是原问题的最优解。图5-8为rk=1、0.1和0.01时φ(X,rk)的曲线。显然,φ所代表的曲线严格地在可行域(X≥0)内。
。显然,当k→∞时,rk→0,X(k)→0。事实上,X*=0也就是原问题的最优解。图5-8为rk=1、0.1和0.01时φ(X,rk)的曲线。显然,φ所代表的曲线严格地在可行域(X≥0)内。
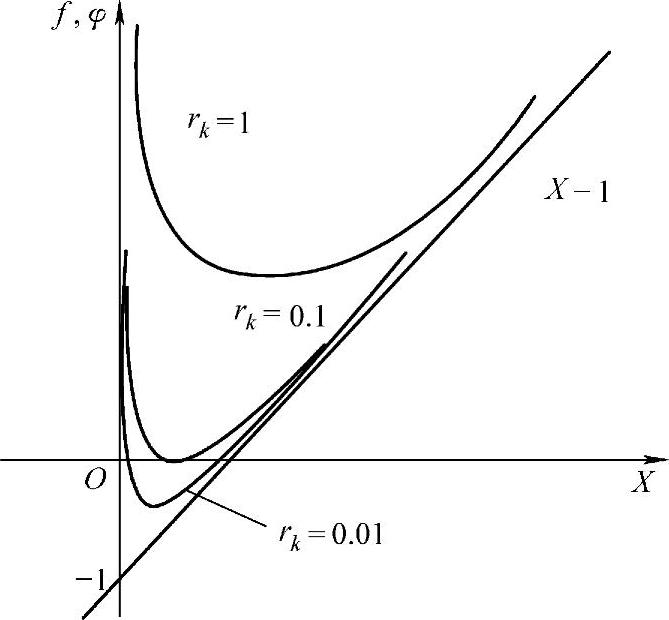
图5-8 例5-6解的几何表示
由上例可见,初始惩罚因子r0的选择对内点法的计算效率影响很大。若r0值选得太小,则在惩罚函数φ(X,rk)中惩罚项的作用就会很小,极值点有可能跑出可行域;反之,则开始几次构造的φ(X,rk)的无约束极值点就会远离约束边界,使计算效率降低。可取r0≈1~5,一般取r0=1。通常,当初始点X(0)是一个严格的内点时,r0可由下式确定:
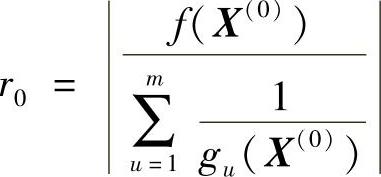
若约束区域是非凸的且X(0)亦不靠近约束边界,则r0可取上式算得值的0.1~0.5倍。
为避免当r0取过大时计算效率降低现象的发生,可增加一个新的约束条件:
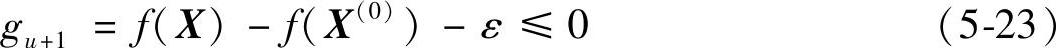
这样,式(5-19)和式(5-20)分别写成:
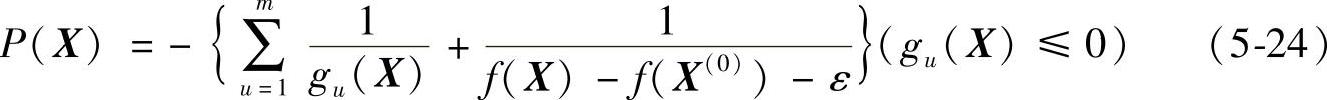
和
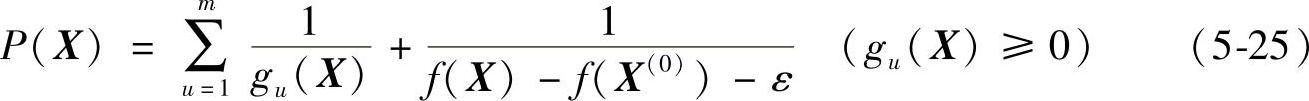
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





