拉格朗日（Lagrangian）乘子法属于约束优化问题的间接解法，其基本思想是将一个约束非线性规划问题转化为一个无约束非线性规划问题来求解。其特点是引入一个待定系数——乘子（Multiplier），构成一个新的无约束条件的目标函数，使数学变换过程简化，而它的最优解即为原目标函数的约束最优解。

以二元函数为例，设目标函数为

f（X）=f（x₁，x₂）

受约束于 h（x₁，x₂）=0

它的极值存在条件为

由上面两式可得

从而有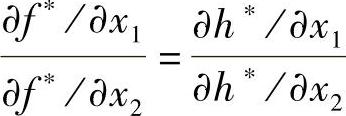

或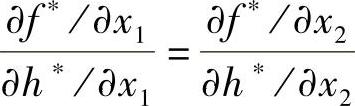

令上式两端为一常数，即得

式中 λ——特定的拉格朗日乘子。

由上式及h（x₁，x₂）=0，得联立方程式：

解此联立方程式，可得极值点x^*₁、x^*₂、λ^*。

求此联立方程组的解相当于求解：(www.daowen.com)

L（x₁，x₂，λ）=f（x₁，x₂）-λh（x₁，x₂）

这一无约束函数的极值点。此函数极值点存在的必要条件为

式中 L（x₁，x₂，λ）——拉格朗日函数。

同理，对n维问题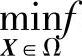：（x₁，x₂，…，x_n）受约束于h_v（X）=0（v=1，2，…，p＜n），则拉格朗日函数为

函数L（X，λ）极小值存在的必要条件为

因为未知数x_i为n个，λ_v为p个，共有n+p个未知数，而恰好有n+p个方程，故能求解。

为了便于在计算机上利用直接寻优方法进行迭代计算，一般引入Z函数

然后对Z函数求极小值，即可求得原问题的最优解。

对于不等式约束优化问题，可设法引入松弛变量，使不等式变成等式，即可按等式约束优化问题求解。例如，对下面不等式约束条件：

引入松弛变量ω，为保证引入项为正值，均用松弛变量的平方，即有

其拉格朗日函数应为