约束坐标轮换法具有算法明了、迭代简单、便于设计者掌握运用等优点。其缺点是,收敛速度较慢;对于维数较高的约束优化问题(如n≥10),很费机时。此外,在某些情况下,还可能出现“死点”的病态,导致输出伪最优点。
现结合图5-5所示的情况来说明出现“死点”的问题。给定初始点X(0)和初始迭代步长h0为某一组数据,按前述的步骤进行迭代。当迭代点到达靠近约束边界的点X(k)时,如图5-5所示,在X(k)点处以步长h0为邻域的4个迭代点X(A)、X(B)、X(C)、X(D)都不能同时满足适用性和可行性的要求,而且即使再缩小h0,其收效甚微,于是X(k)必将作为最终结果从计算机输出。X(k)就是一个死点。显然。它是一个伪最优点。
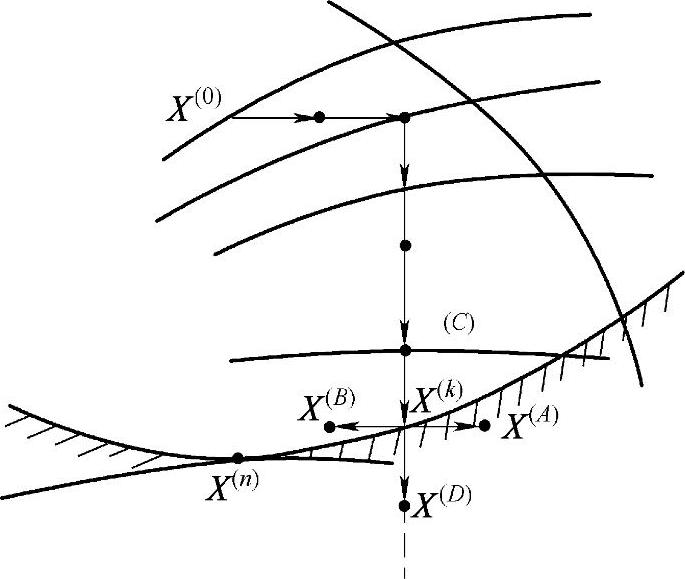
图5-5 约束坐标轮换法的“死点”
为了辨别输出最优点的真伪,可以用K-T条件来检验。通常的做法是,输入多个初始点,并给出各种不同的初始步长进行多次运算,再从众多的输出解中进行比较而排除伪最优点。
【例5-2】 用约束坐标轮换法求解
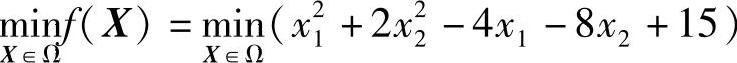
Ω:g1(X)=9-x21-x22≥0
g2(X)=x1≥0
g3(X)=x2≥0的最优解。
解(1)取初始点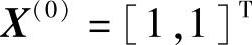 ,初始步长h0=0.5,比例因子μ=2.0,收敛精度ε=0.1。
,初始步长h0=0.5,比例因子μ=2.0,收敛精度ε=0.1。
(2)因gj(X(0))≥0(j=1,2,3),故X(0)是可行点。这时f(X(0))=6.00。
(3)沿e1方向搜索
第一步 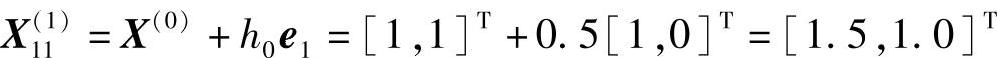
因为 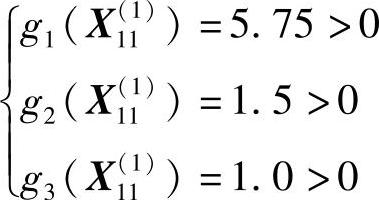
故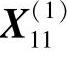 是可行点。
是可行点。
又 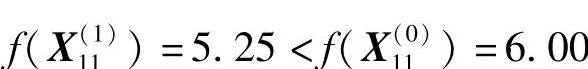
因此沿该方向加速前进,取2h0=1.0。
第二步 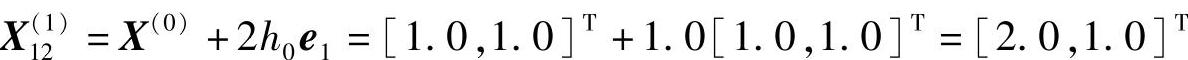
同理可检查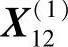 是可行点,且
是可行点,且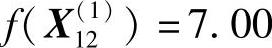 。
。
因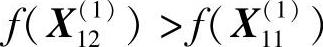 ,故停止前进,退回点
,故停止前进,退回点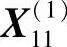 ,记为
,记为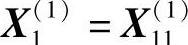 。
。
(4)沿第二坐标轴(e2)方向搜索
第一步 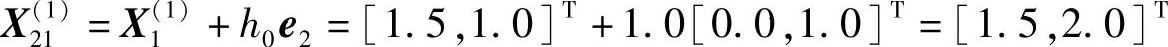
可验证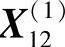 是可行点,且
是可行点,且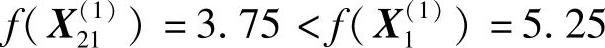 ,故沿该方向加速前进,即取2h0=1.0。
,故沿该方向加速前进,即取2h0=1.0。
第二步 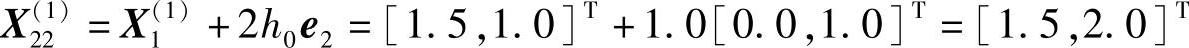
可验证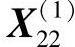 是可行点,且
是可行点,且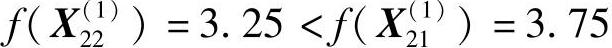 。于是,沿该方向再加速前进,取4h0=2.0
。于是,沿该方向再加速前进,取4h0=2.0
第三步 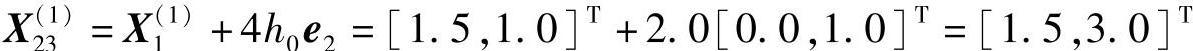 可验证
可验证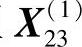 为非可行点,故退回点
为非可行点,故退回点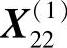 ,记为
,记为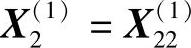 。至此即完成第一轮搜索,以X2(1)为初始点,进行下一轮搜索。
。至此即完成第一轮搜索,以X2(1)为初始点,进行下一轮搜索。
(5)沿e1方向搜索
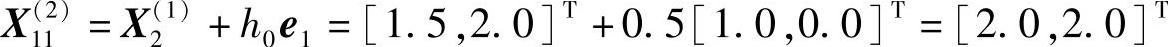
可验证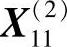 为可行点,且
为可行点,且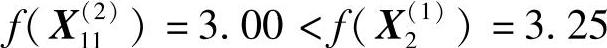 ,故沿该方向加速前进,即
,故沿该方向加速前进,即
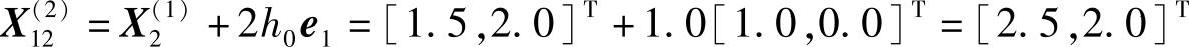 (https://www.daowen.com)
(https://www.daowen.com)
可验证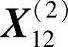 为非可行点,舍弃。退回到点
为非可行点,舍弃。退回到点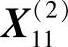 ,记为
,记为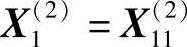 。
。
(6)沿e2方向搜索
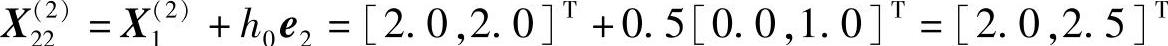
可验证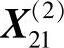 是非可行点,表明沿e2正方向试探失败,改沿e2的负方向搜索,即
是非可行点,表明沿e2正方向试探失败,改沿e2的负方向搜索,即
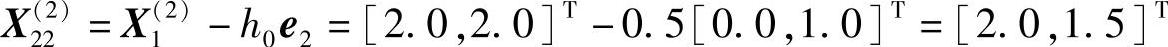
可验证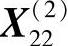 是可行点,但
是可行点,但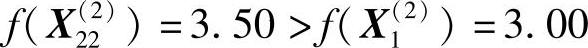 ,故舍弃
,故舍弃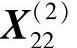 ,退回到点
,退回到点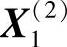 ,记为
,记为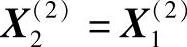 ,进行第三轮搜索。
,进行第三轮搜索。
(7)沿e1方向搜索
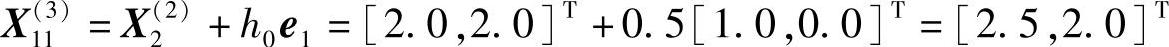
因点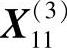 是非可行点,故必为沿e1负方向搜索
是非可行点,故必为沿e1负方向搜索
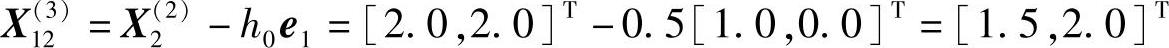
点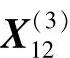 是可行点,但
是可行点,但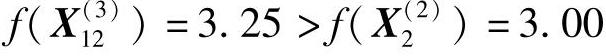 ,故沿e1正、负方向试探均失败,记为
,故沿e1正、负方向试探均失败,记为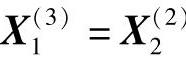 。
。
(8)沿e2方向搜索
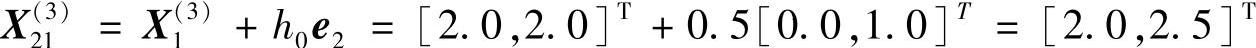
点X21(3)为非可行点,故改沿e2负方向搜索,即
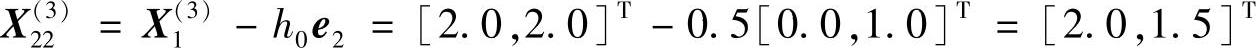
点X21(3)虽为可行点,但f(X22(3))=3.5>f(X1(3))=3.00,故退回点X1(3),记为X2(3)=X1(3)。在这一轮循环中,因初始点X2(2)与最终点X2(3)相同,故收缩步长,即取h0=h0/μ=0.5/2=0.25,然后进行第四轮循环。
(9)沿e1方向搜索
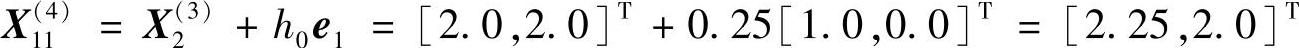
因X11(4)为非可行点,故改沿e1负方向搜索,即
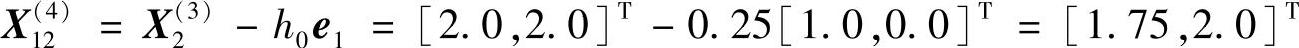
可验证X12(4)为可行点,但f(X12(4))=3.0625>f(X2(3))=3.00,故记为X1(4)=X2(3)。
(10)沿e2方向搜索
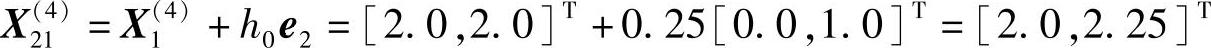
因X2(14)为非可行点,故沿e2负方向搜索,即
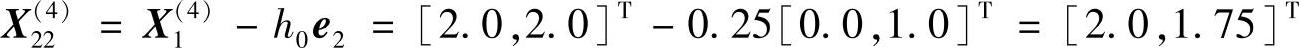
X22(4)虽为可行点,但f(X22(4))=3.125>f(X1(4))=3.00,退回到X1(4),记为X2(4)=X(4)1。
因X2(3)=X2(4),故再次收缩步长,取h0=h0/μ=0.5/4=0.125,然后进行第五轮循环。通过类似计算,结果为X2(5)=X2(4),再收缩步长,取h0=h0/μ=0.0625,进行第六轮循环。计算后,得最终点为X2(6)=[2.0,2.0]T,与初始点相同,且因h0=0.0625<ε=0.1,故停止计算,得最优解X=[2.0,2.0]T,f(X)=3.00。
利用解析法可求得原问题的理论最优解,也是X=[2.0,2.0]T,f(X)=3.00。
由以上寻优的迭代过程可看出,约束坐标轮换法的收敛快慢以及能否收敛,不仅与初始点及初始步长有较大关系,而且在一定程度上依赖于目标函数的性态。如果目标函数的二次性强,该方法就收敛快,否则就收敛较慢。此外,可行域的形状对该方法的收敛速度也有影响。如可行域窄小细长,则收敛很慢。
总而言之,尽管约束坐标轮换法存在着上述缺点及可能出现伪最优点,但由于该方法具有逻辑简明,算法易懂,便于学习者掌握等优点,因而仍常用来求解维数较低(n<5)、不含等式约束的优化设计问题。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






