图5-3所示为二维约束优化问题的坐标轮换法图解。如图，首先在可行域Ω内任取一个初始点X^（0）。以X^（0）为起点，取一个适当的初始步长h₀，h⇐h₀，按迭代式X₁^（1）=X^（0）+he₁取得沿x₁坐标轴正向的第一个迭代点。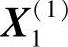

检查该点的适用性和可行性。即检查

如果两者均满足，则步长加倍

h⇐2h

再按迭代式

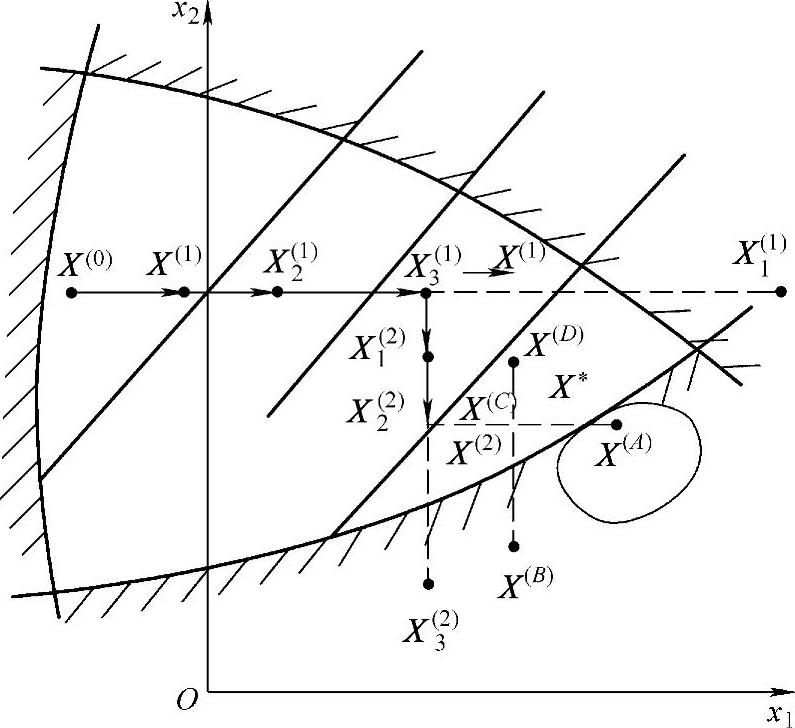
图5-3 二维约束坐标轮换法迭代过程

获得沿X₁轴正向的第二个迭代点X₂^（1）。对同时满足适用性和可行性条件的新迭代点。均可倍增步长后按迭代式

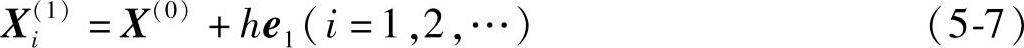(www.daowen.com)

不断产生迭代点。

若不满足可行性条件，但满足适用性条件，如图5-3所示的X₃^（1）、X₃^（2），则取它的前一迭代点（如X₃^（1）和X₂^（2））作为沿该方向搜索的终点，转而改为沿另一坐标轴正向进行搜索。

若满足可行性条件但不满足适用性条件，则采用负步长h⇐-h₀进行迭代。

循环地沿各坐标轴方向进行迭代，直到点列X^（1）、X^（2）…逐步逼近约束最优点X^*为止。

当迭代点到达X^（k）时出现如下情况：不论沿e₁或e₂方向，也不论取正步长h₀或负步长-h₀，X^（k）邻近的4个点X^（A）、X^（B）、X^（C）、X^（D）都不能同时满足适用性和可行性条件。此时，X^（k）即可作为约束最优点输出。若要获得精度更高些的解，还可以缩减初始步长h₀⇐h₀/μ（μ可取正整数）后继续迭代，直至当h₀≤ε时才输出X^*并停止计算。

对于n维约束优化问题，其迭代过程是相同的。即依次沿各坐标轴方向e₁，e₁，…，e_n按加速步长进行一维搜索，并反复循环。当初始步长已缩小到h₀≤ε，且在X^（k）点沿n个坐标轴方向取正、负步长的各迭代点均不能同时满足适用性和可行性时，则X^（k）就可作为约束最优点X^*输出。

图5-4是约束坐标轮换法的迭代过程框图。

图5-4 约束坐标轮换法程序框图