复合形法的迭代步骤如下:
(1)确定初始可行点 对于问题较简单的情况,如找不到k个可行点,可凭经验选出。但对复杂(变量较多)的问题,要用随机方法产生初始可行点,即

若X(1)为可行点,则进行(2)。
(2)随机产生其他顶点

式中 i——点数,i=2,3,…,k;
j——点的坐标,j=1,2,…,n。
(3)构成复合形 若已经产生了的k个顶点中有L个可行点,其余k-L个顶点为不可行点,则继续产生第L+1个点,如果这个点为可行点,再继续产生新点,即第L+2个点;否则,将该点取为
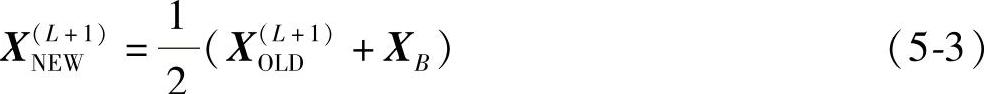
式中 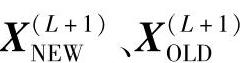 ——分别为第L+1个点的新点和旧点;
——分别为第L+1个点的新点和旧点;
XB——前L个点的中心点。
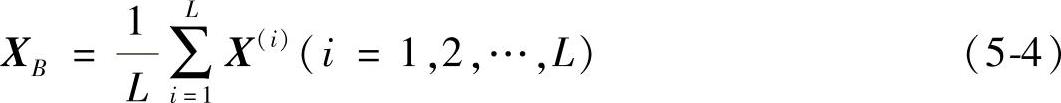
重复此过程直至X(L+1)点成为可行点。
按上述方法产生的k个可行点即构成了复合形。
(4)寻求映射点 计算复合形所有顶点的函数值,取其中最大者为最差点XH,最小者为最好点XL。
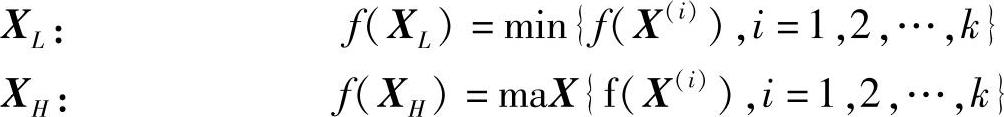
计算除XH外的k-1个顶点的形心XC,即

如果XC不是可行点,则以k个顶点中最好点XL为下界,以XC为上界重新利用随机数选点,构成复合形,重复(1)~(4)的过程。
如果XC是可行点,则在由XH至XC点的方向上,取一映射点XR,即

式中 α——映射系数,一般可取α=1.3。
若XR为不可行点,则须将XR点收缩回来,即使α减半,重算XR,直至XR是可行点为止。
(5)比较目标函数值 若f(XR)<f(XH),则以XR代替XH,构成新复合形,返回进行(4)。
若f(XR)>f(XH),则将α减半,直至f(XR)<f(XH),返回(4)。若α虽不断减半,直到小于预先给定的ξ时,f(X)仍无改进,则将(4)选择的XH改成次差点XC,即
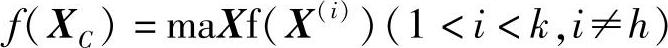
这样,由次差点出发求映射点,重复上述过程。
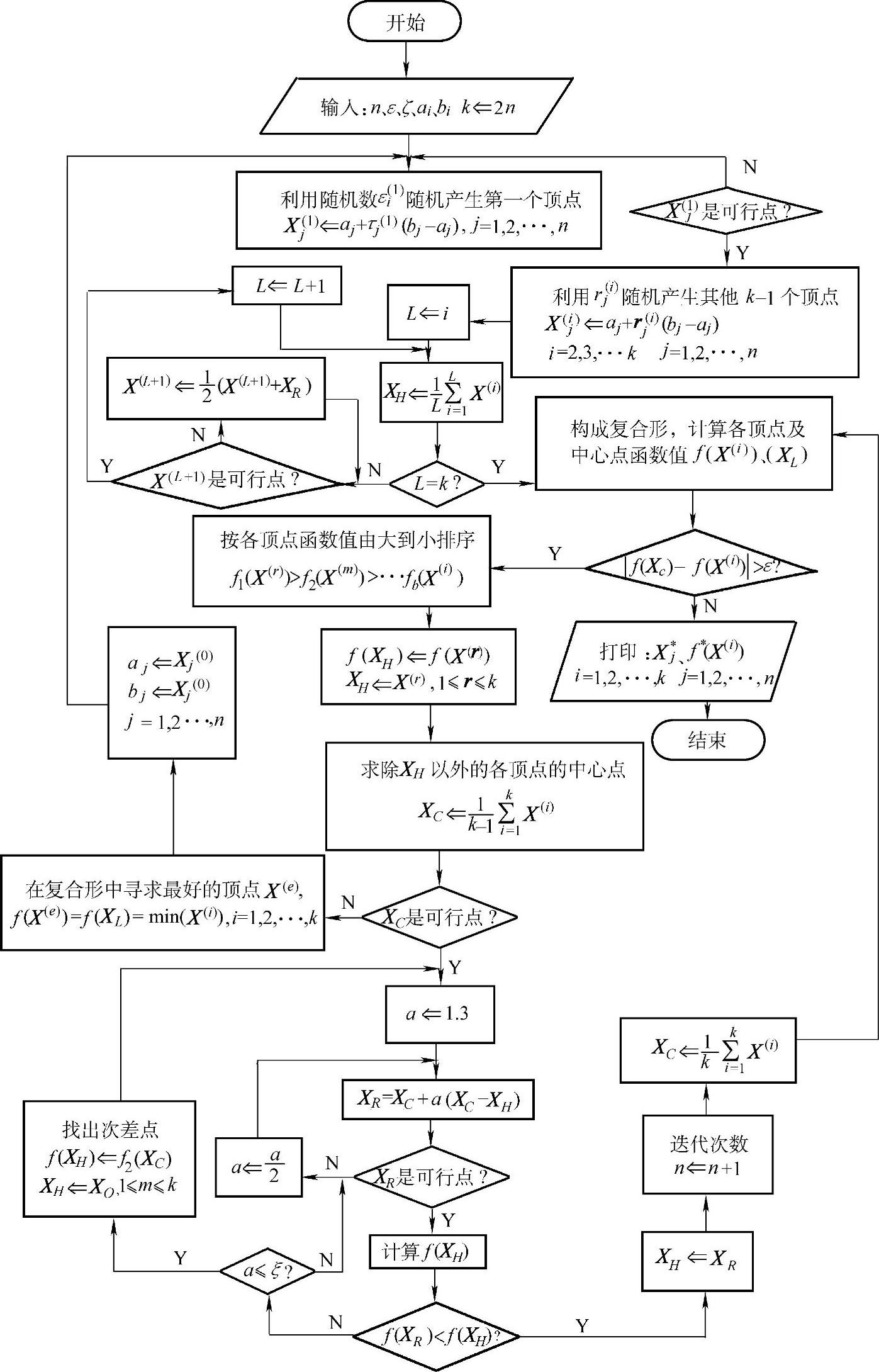
图5-2 复合形法程序框图
(6)检验停机准则
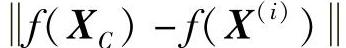 ≤ε(i=1,2,…,k)或
≤ε(i=1,2,…,k)或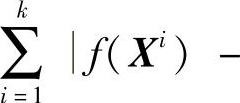 f(XL)≤ε是否满足。若满足,则认为目标函数已经收敛,可终止迭代,返回(4)。
f(XL)≤ε是否满足。若满足,则认为目标函数已经收敛,可终止迭代,返回(4)。
复合形法的迭代过程如图5-2所示。
【例5-1】 试用复合形法求解目标函数f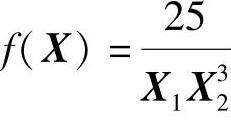 的极小值,已知约束条件为(www.daowen.com)
的极小值,已知约束条件为(www.daowen.com)
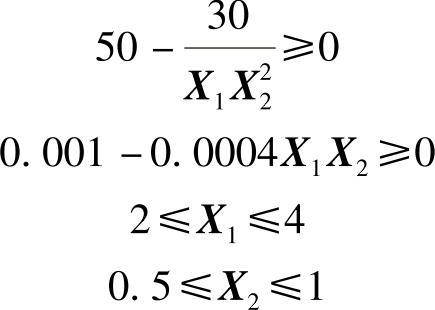
解 取复合形的顶点数k=2n=4,用随机法产生初始复合形的顶点,取随机数
r11=0.1,r21=0.2,r31=0.3,r41=0.4
r12=0.1,r22=0.2,r32=0.3,r42=0.4则初始复合形4个顶点的X1坐标分量为[式(5-2)]
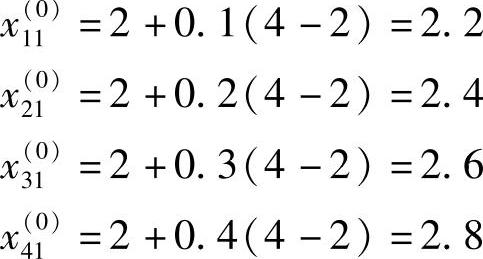
4个顶点的X2坐标分量为[式(5-2)]

则初始复合形4个顶点的坐标为
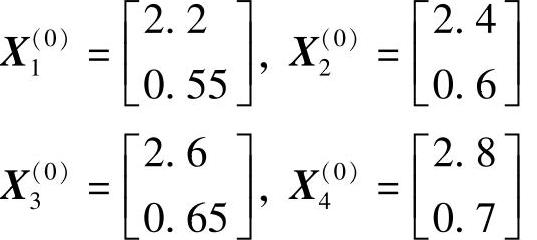
检验各顶点是否可行:将各顶点的坐标值代入各约束方程,均满足约束条件。
1)计算各顶点的函数值并比较它们的大小:
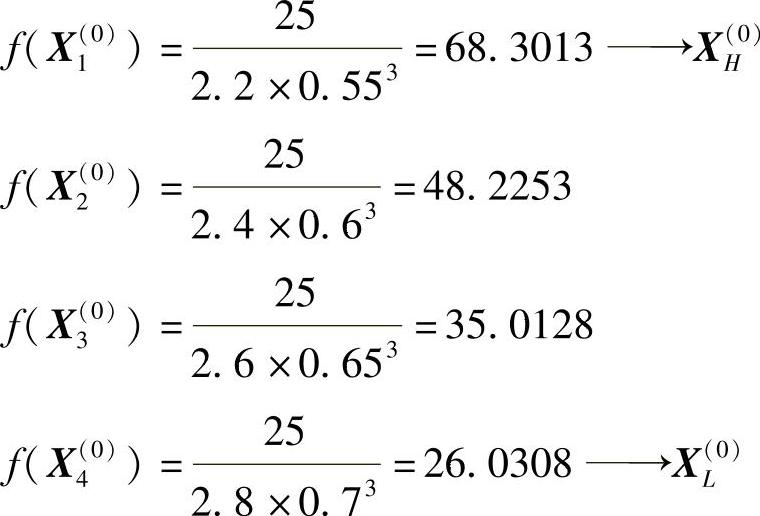
2)求除最差点外其余三点的形心[式(5-5)]:
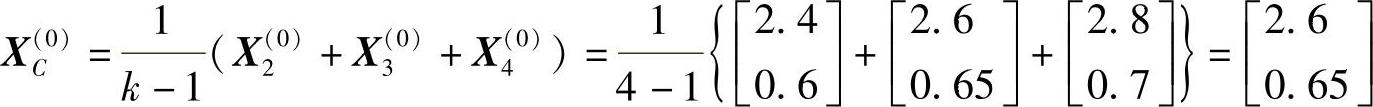
代入约束条件,证明在可行域内。
3)求最差点的反射点,按式(5-6),α=1.3:
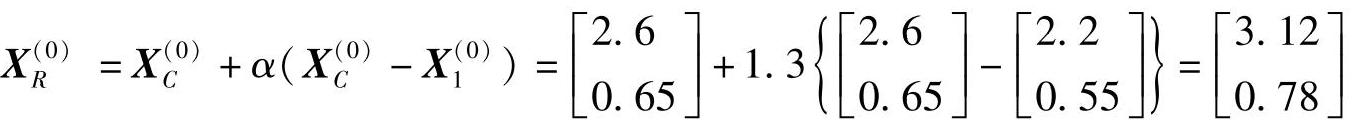
(可证明在可行域内)
4)计算f(XR(0))并与f(XH(0))比较:
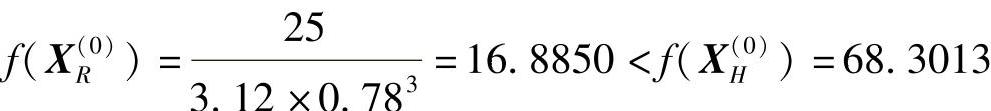
故可用新点XR(0)替换X1(0),构成新的复合形:
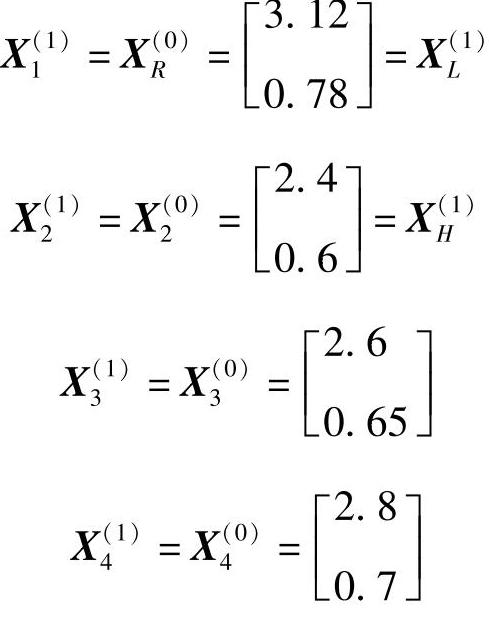
5)计算新复合形中除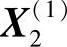 外各顶点的形心
外各顶点的形心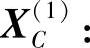
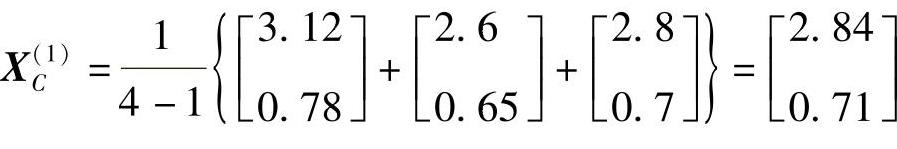
代入约束方程知,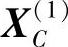 在可行域内。
在可行域内。
6)计算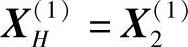 的反射点
的反射点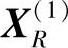 ,取α=1.3:
,取α=1.3:
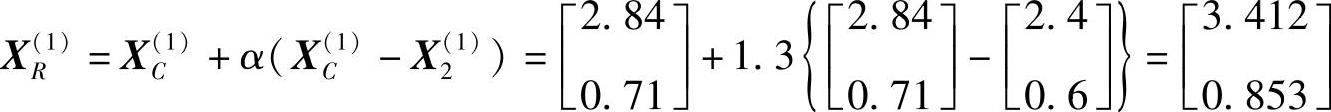
代入约束条件,表明不满足第二个约束条件,故应将α减半,即取α=0.65,重算反射点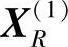 :
:
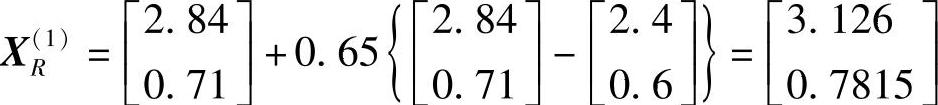
代入约束条件,表明符合约束要求。
7)计算新反射点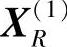 的函数值:
的函数值:
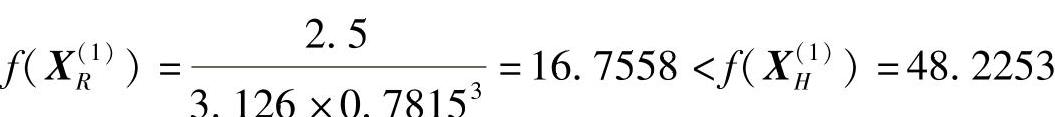
故可用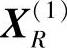 替换
替换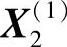 ,构成新的复合形。依次重复上述步骤,直至满足预定的计算精度为止,取复合形各顶点函数值最小值为最优解。
,构成新的复合形。依次重复上述步骤,直至满足预定的计算精度为止,取复合形各顶点函数值最小值为最优解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

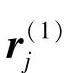 ——在区间[0,1]内
——在区间[0,1]内





