鲍威尔法的迭代步骤如下：

1）给定初始点X^（0）∈Eⁿ，置f（X^（0））⇒f₀；给定允许误差ε＞0，n个初始方向为：S^（1）=e₁，S^（2）=e₂，……，S^（n）=e_n。

2）从X^（0）出发，依次沿坐标轴e_i（i=1，2，…，n）方向进行一维搜索，即

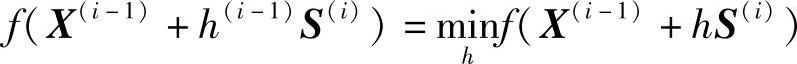
令 X^（i）=X^（i-1）+h^（i-1）S^（i）

f（X^（i））=f_i

3）判断是否i=n，若是，进行4）；若i＜n，则置i+1⇒i，返回2）。

4）检验是否满足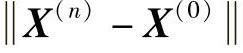＜ε，若满足，则停止迭代，得X^*=X（n）；否则进行5）。

5）比较f_i-f_i+1的大小，用Δ表示其中最大者，即令

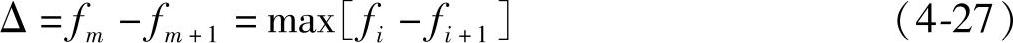
式中，0≤i≤n-1，0≤m≤n-1。并记下m及m+1。

6）将X^（0）和X^（n）间的连线延长1倍，得新点和新的目标函数值，即

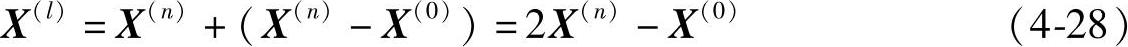
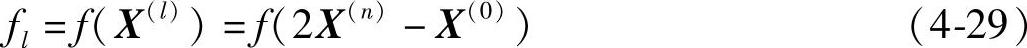
7）判别是否满足：

若满足，则令f（X^（n））⇒f₀，X^（n）⇒X^（0），1⇒i，返回进行2）；否则进行8）。

8）令S^（i）⇒S^（i）（i=1，2，…，n）

S^（i+1）⇒S^（i）（i=m+1，m+2，…，n-1）

又令X^（n）-X^（0）=S^（n），且在此方向S^（n）上进行关于h的一维搜索，即

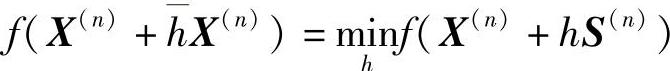
令 X^（0）=X^（n）+hS^（n）

f（X^（0））⇒f₀，1⇒i

返回进行2）。

鲍威尔法的迭代过程如图4-11所示。

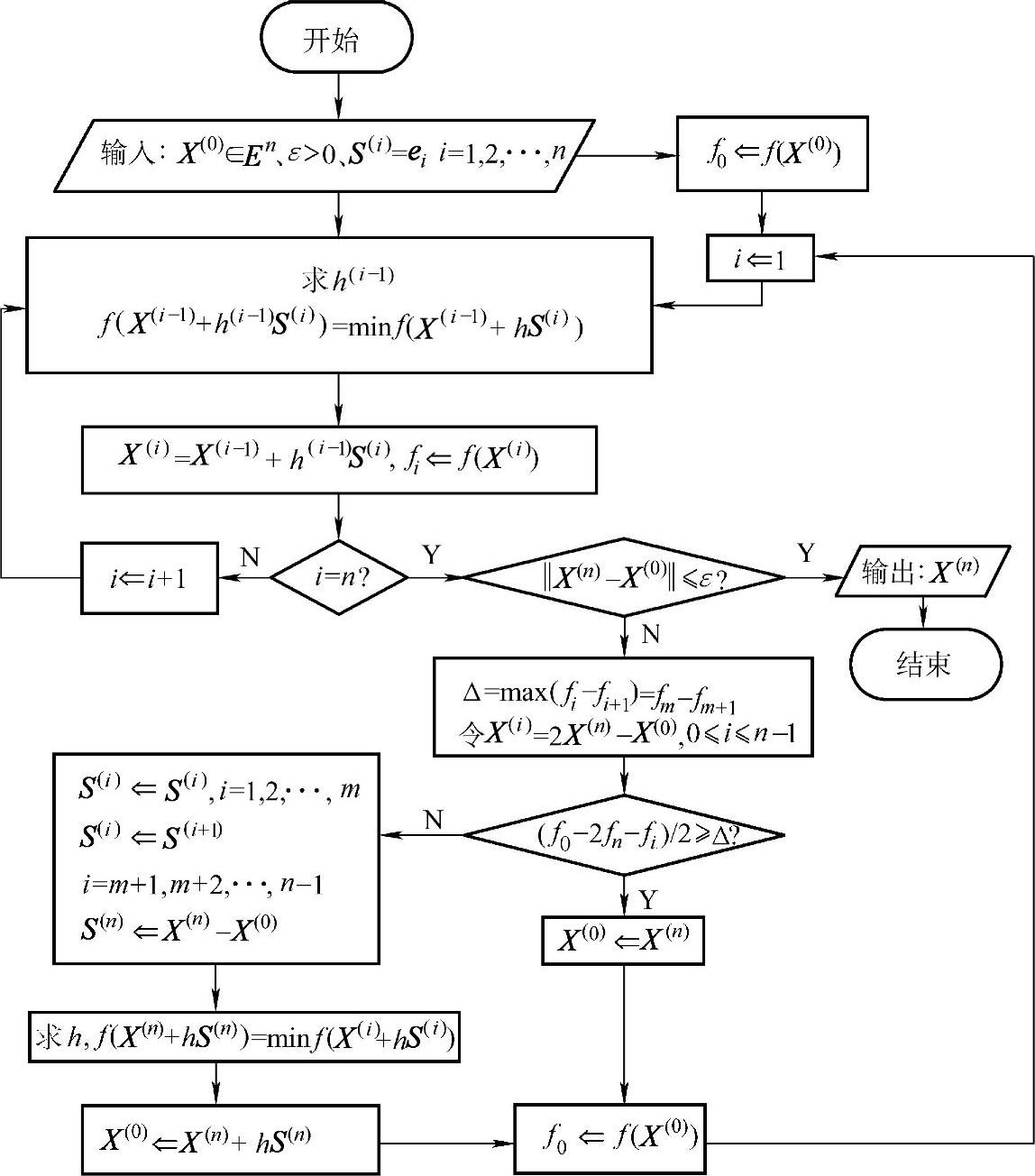
图4-11 鲍威尔法程序框图

【例4-8】试用鲍威尔法求函数f（X）=11x²₁+11x²₂+18x₁x₂-100x₁-100x₂+250的极小值。

解（1）给定初始点X^（0）=[0，0]^T，f（X^（0））=250=f₀。第一次迭代方向为

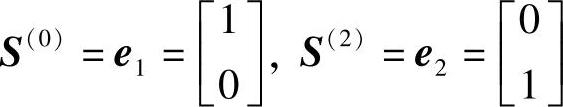
（2）从X^（0）出发，沿e_i（i=1，2）依次进行一维搜索。由

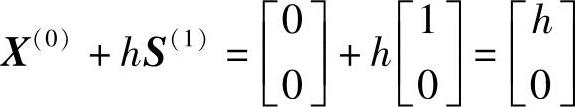
得到 f（X^（0）+hS^（1））=11h²-100h+250

令 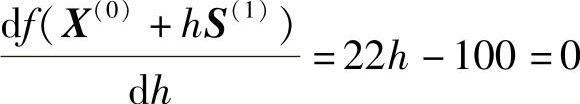(www.daowen.com)

求得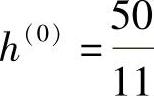

则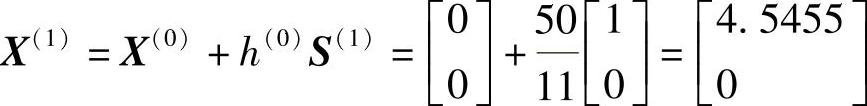

f（X^（1））=22.7273=f1

再由X^（1）出发沿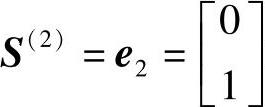方向进行一维搜索，由

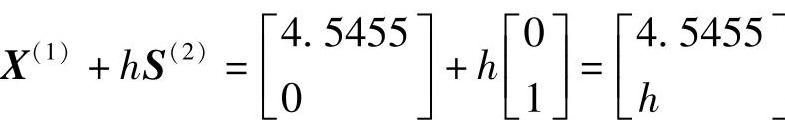
得到f（X^（1）+hS^（2））=11×4.5455²+11h²+18×4.5455h-100×4.5455-100h+250

令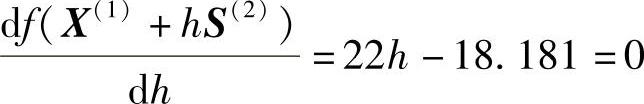

求得 h（1）=0.8264

则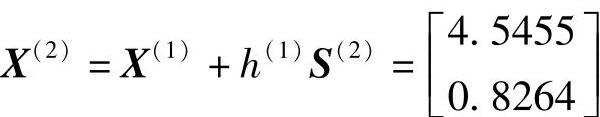

f（X^（2））=15.2148=f₂

（3）判断是否满足i=n。因为i=2，n=2，故i=n，进行（4）。

（4）检验是否满足

（5）比较f_i-f_i+1的大小：

f₀-f₁=250-22.7273=227.2727

f₁-f₂=22.7273-15.2148=7.5125

取最大者：

Δ₁=f₀^-f1=227.2727

并记下m=0，m+1=1

（6）求新点X^（l）：

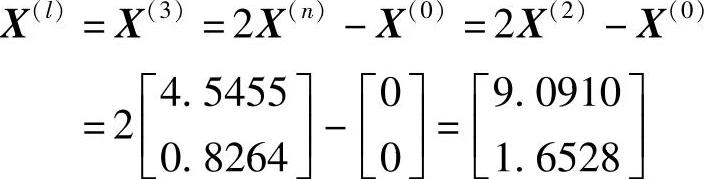
f（X^（l））=f（X^（3））=385.2392=f_l=f₃

（7）判断是否满足（f₀-2f_n+f_l）/2≥Δ₁

因为f（X^（3））＞f（X^（2）），所以X^（3）并非为好点，X^（2）-X^（0）并非为好方向。于是仍要沿S^（1）=e₁和S^（2）=e₂方向进行搜索。令

f（X^（2））=f₀，X^（2）=X^（0）

返回进行（2）（下面迭代时将X^（i）记为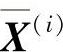，过程从略）。当进行到（7）时，因所得

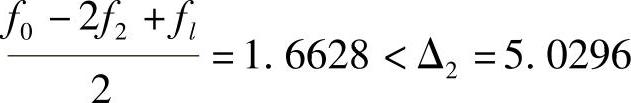
说明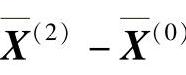为好方向。于是下一轮迭代方向应去掉m+1方向，即S^（1）=e₁的方向，则迭代方向为

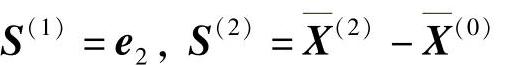
重复上述步骤，得到近似最优解为

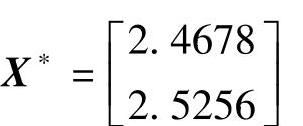
f（X^*）=0.0035