单纯形法的迭代步骤如下:
1)给定维数n,允许误差ε1>0,ε2>0,压缩系数λ(0<λ<1,但λ≠0.5,一般取为0.25或0.75),扩张系数μ(一般μ=1.2~2)。
2)计算初始单纯形顶点Xi(0)及其函数值f(Xi(0)):
先选定一个初始点X0(0),初始步长h>0,其余顶点为
Xi(0)=X(0)+hei(i=1,2,…,n) (4-19)
式中,ei为第i个单位坐标向量。H一般取为0.5≤h≤15。置0⇒k。
3)比较各顶点函数值的大小,选出最好点XL,最差点XH和次差点XG,即
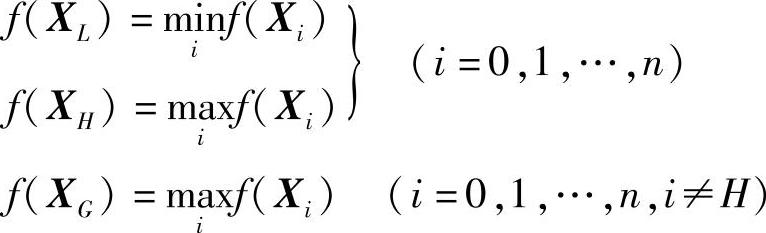
4)检查是否满足收敛准则:
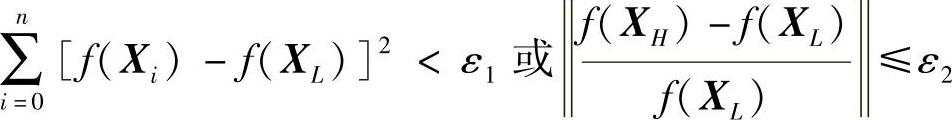
若满足,则输出XL=X*和f(XL)=f(X*);否则进行5)。
5)计算除XH点外n个顶点的几何中心:
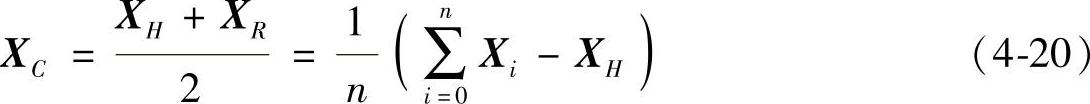
由上式求出反射点:
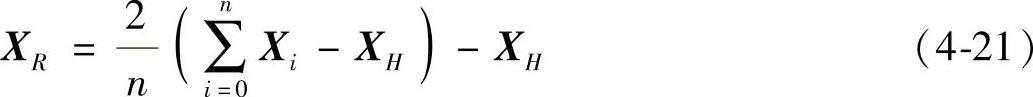
6)若f(XR)≥f(XG),则压缩步长,令
XS=(1-λ)XH+λXR (4-22)
计算f(XS),转向7);若f(XR)<f(XG),则加大步长,令
XS=(1-μ)XH+μXk (4-23)
计算f(XE),转向8)。
7)若f(XS)<f(XG),则转向9);否则将单纯形向XL点缩小一半,并计算除XL点外各点的坐标:
Xi=(Xi+XL)/2(i=1,2,…,n)
组成缩小了的单纯形,转向10)。
8)若f(XE)<f(XR),则XE⇒XS,f(XE)⇒f(XS);否则XR⇒XS,f(XR)⇒f(XS)。
9)舍弃XH点,以XS点和其余n个顶点构成新的单纯形。
10)置k+1⇒k,返回3)。(www.daowen.com)
单纯形法的迭代过程如图4-7所示。
【例4-6】 试用单纯形法求目标函数f(X)=60-10x1-4x2+x21+x22-x1x2的极小值。
解(1)给定ε=0.001,λ=0.75,μ=2。
(2)计算初始单纯形顶点Xi(0)及其函数值f(Xi(0))。
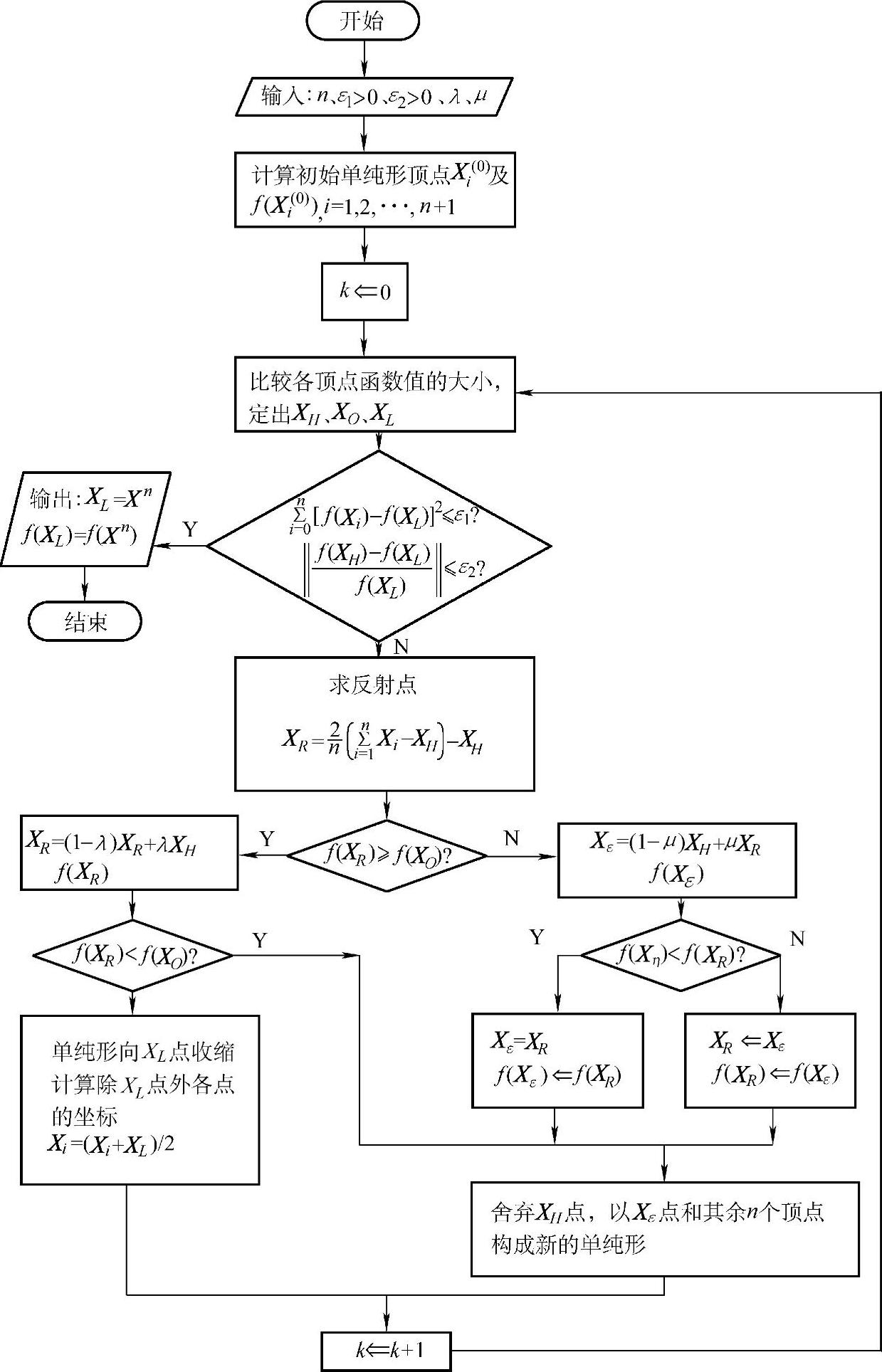
图4-7 单纯形法程序框图
设X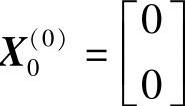 ,初始步长h=2,则
,初始步长h=2,则
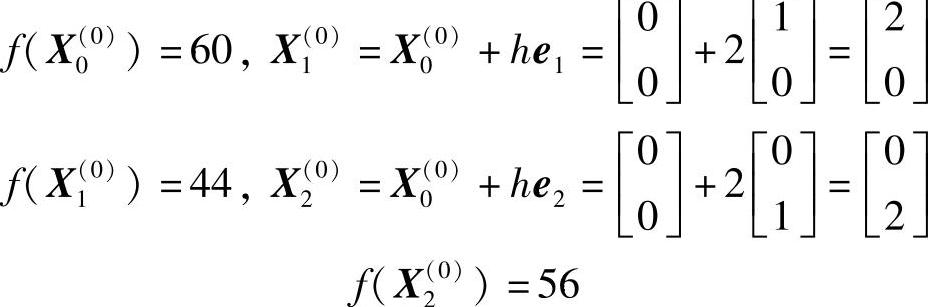
于是 f(XH)=f(X0(0))=60,f(XG)=f(X2(0))=56
f(XL)=f(X1(0))=44
(3)检查停机准则:
因为 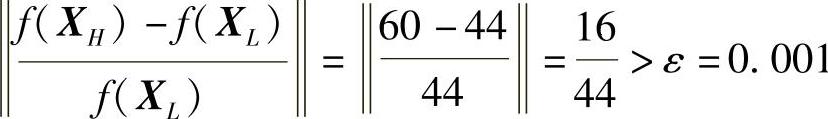
所以进行(4)。
(4)求反射点XR:
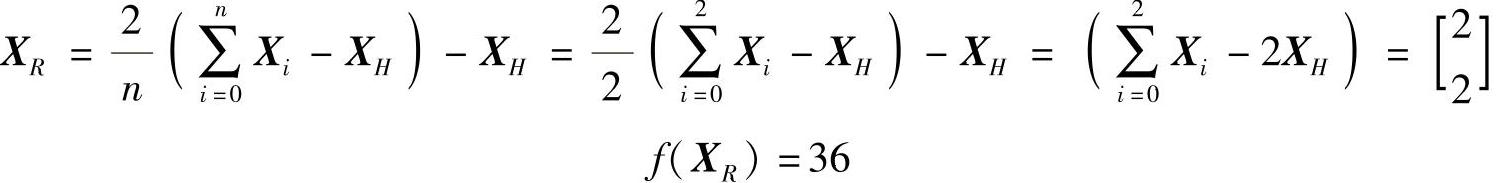
(5)因为f(XR)<f(XG),所以加大步长:
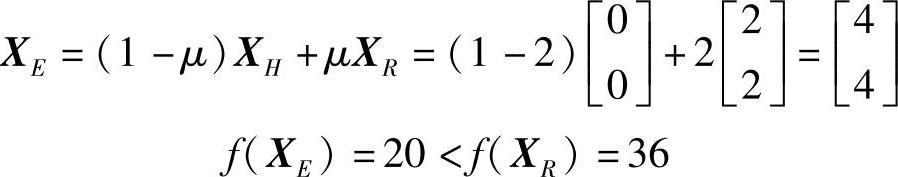
则 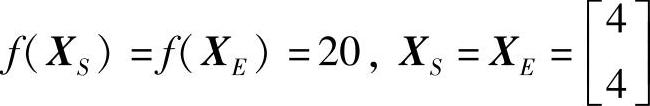
舍弃原来的XH=X0(0)点,取XS、X1(0)和X2(0)组成新的单纯形,其为: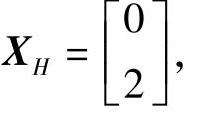
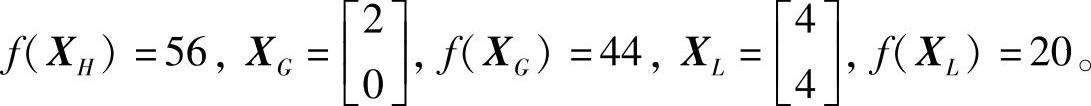
重复上述步骤,迭代至第13次得到:
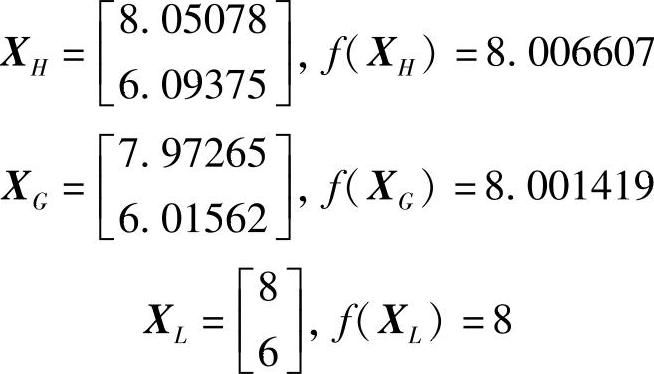
因为 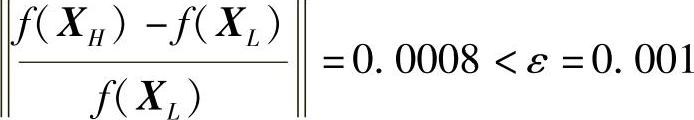
故满足了停机准则,最优解为
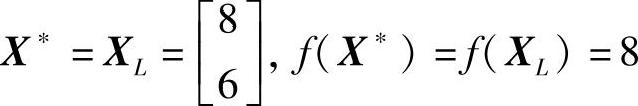
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





