如前所述，直接解法（单纯形法、坐标轮换法和鲍威尔（Powell）法）中只用到函数f（X），而不涉及其导数，这对于一些求导困难的函数的情形，无疑是适合的。

所谓n维欧氏空间Eⁿ中的单纯形，是指在n维空间中由n+1个线性独立的点构成的简单图形或凸多面体。例如，在一维空间中由两点构成的线段；在二维空间中由不在同一直线上的三个点构成的简单图形即三角形；在三维空间中由不在同一平面上的四个点构成的四面体；在n维空间中由n+1个顶点构成的凸多面体等。

根据问题的维数n，选取n+1个顶点构成的单纯形，求出这些顶点处的目标函数值并加以比较，确定它们当中有最大值的点及函数的下降方向，设法寻找一新的比较好的点替换那个有最大值的点，从而构成新的单纯形。随着这种取代过程的不断进行，新的单纯形将向着极小点收缩，即可得到满足收敛准则的近似解。这就是单纯形法的基本思想。

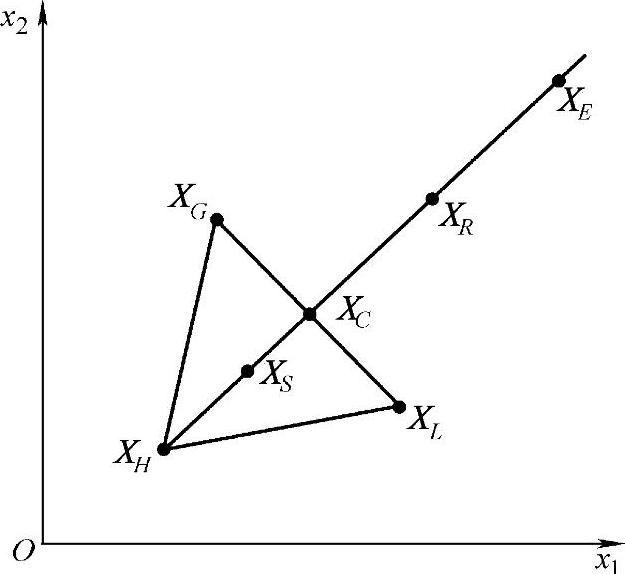
图4-6 单纯形法图解

对于如图4-6所示的二维情形，单纯形的三个顶点为X_G、X_H、X_L，算出相应的函数值f_G、f_H、f_L。若

f_H＞f_G＞fL(www.daowen.com)

则说明X_H最差，X_L最好。故应丢掉X_H点而另寻新点，以构成新的单纯形。将X_H与线段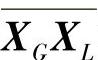的中点X_C连结并延长之，在延长线上取一点X_R，使

X_R=X_C+α（X_C-X_H） （4-18）

式中α称为反射系数，一般取α=1。上述过程也称为反射过程，X_R称为X_L关于X_C的反射点。

计算出f_R，若f_R＜f_G，则可沿延长线走得更远些，取X_E，这一过程称为扩张。若f_E≤f_R则取X_E为新点，否则取X_R为新点。若f_R≥f_G，说明可能前进得太远了，须要压缩步长，如取X_S点，这一过程称为收缩。

形成新的单纯形后，再重复以上步骤，直到满足给定的收敛条件为止。