如前所述，DFP变尺度方法对于高维问题具有收敛速度快、效果好等优点，但亦同时存在数值稳定性方面不够理想的缺陷，如舍入误差和一维搜索不精确等，有时会因此而使某个构造矩阵A^（k）不能保持正定或变为奇异而导致计算失败。为此，人们致力于寻求改进方法。20世纪70年代初，Broydon、Fletcher、Gol-dstein和Shanno导出一种更为稳定的构造矩阵迭代公式，此即为著名的BFGS变尺度公式。

BFGS变尺度法的迭代关系和DFP法相同，仍通过修正矩阵E^（k）来求近似矩阵A^（k+1），即

A^（k+1）=A^（k）+E^（k）

其中，E^（k）可由下式表示：

式中，ΔX^（k）和ΔG^（k）的迭代关系与式（4-13）相同。而系数ξ_k则由下式确定：

比较式（4-12）和式（4-15），BFGS法在构造矩阵计算方面较为复杂，但正是这种补充和修正使得所形成的构造矩阵不易变为奇异，因而具有更好的数值稳定性，是目前公认的一种最好的变尺度法。

BFGS变尺度法的性质、基本思想和迭代步骤均与DFP变尺度法相同。

【例4-5】试用BFGS法求无约束问题。

取初始点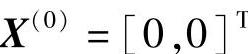，精度要求ε=0.001。

解 目标函数的梯度向量为

Δf（X）-[3x₁-x₂-2，x₂-x₁]^T

采用精确的一维搜索：

X^（k+1）=X^（k）+h^（k）S^（k）

其中步长h^（k）由下式(www.daowen.com)

导出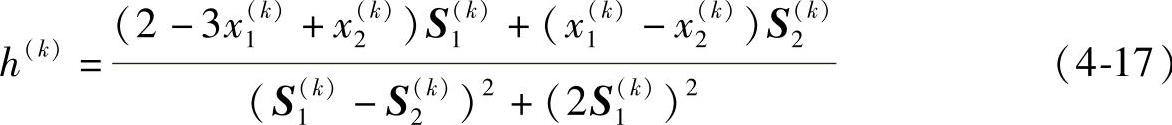

取初始矩阵对称矩阵

进入第一次迭代，计算得

因为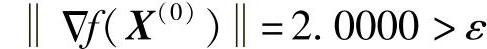

不满足终止准则。计算搜索方向

再由式（4-17），求得步长h（0）=0.3333。置

则G^（1）=Δf（X^（1））=[-0.0002，-0.6666]T

计算ΔG^（0）=G^（1）-G^（0）=[1.9998，-0.6666]^T

ΔX^（0）=X^（1）-X^（0）=[0.6666，0.0000]^T

把上述结果代入式（4-15）和式（4-16），得

转入第二次迭代，经计算得

满足终止准则，停止计算，得本问题的近似最优解为X^*=X^（2）=[1.0001，1.0000]^T，f（X^*）=-1。