【摘要】:共轭梯度法的迭代步骤如下:1)给定初始点X∈E*,允许误差ε>0。3)令S=-Δf,置0k。 试用共轭梯度法求目标函数f=x21+x22-x1x2-10x1-4x2+60的极小点。图4-4 共轭梯度法程序框图解 给定初始点因为在初始点处的梯度所以进行迭代计算。第一次迭代计算:取利用一维搜索,求得h≈0.763157894,则所以进行下一次迭代。第二次迭代计算:因为k=1<n=2,所以计算β:取然后利用一维搜索求得h=0.436781609,则检验是否满足收敛准则,即因达到精度要求,故停止迭代计算,结果为
共轭梯度法的迭代步骤如下:
1)给定初始点X(0)∈E*,允许误差ε>0。
2)检验是否满足收敛准则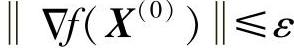 ,若满足,则X*=X(0);否则,进行3)。
,若满足,则X*=X(0);否则,进行3)。
3)令S(0)=-Δf(X(0)),置0⇒k。
4)利用式(4-7)求h。
5)利用式(4-6)求X(k+1)。
6)检验是否满足收敛准则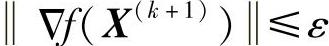 ,若满足,则X*=X(k+1);否则进行7)。
,若满足,则X*=X(k+1);否则进行7)。
7)判别k=n(n为目标函数的维数)是否成立,若k=n,则令X(n+1)⇒X(0),返回进行3);否则(即k<n),计算β(k),并取
S(k+1)=-Δf(X(k+1))+β(k)S(k) (4-9)
令k+1⇒k,返回进行4)。
共轭梯度法的迭代过程如图4-4所示。
【例4-3】 试用共轭梯度法求目标函数f(X)=x21+x22-x1x2-10x1-4x2+60的极小点。
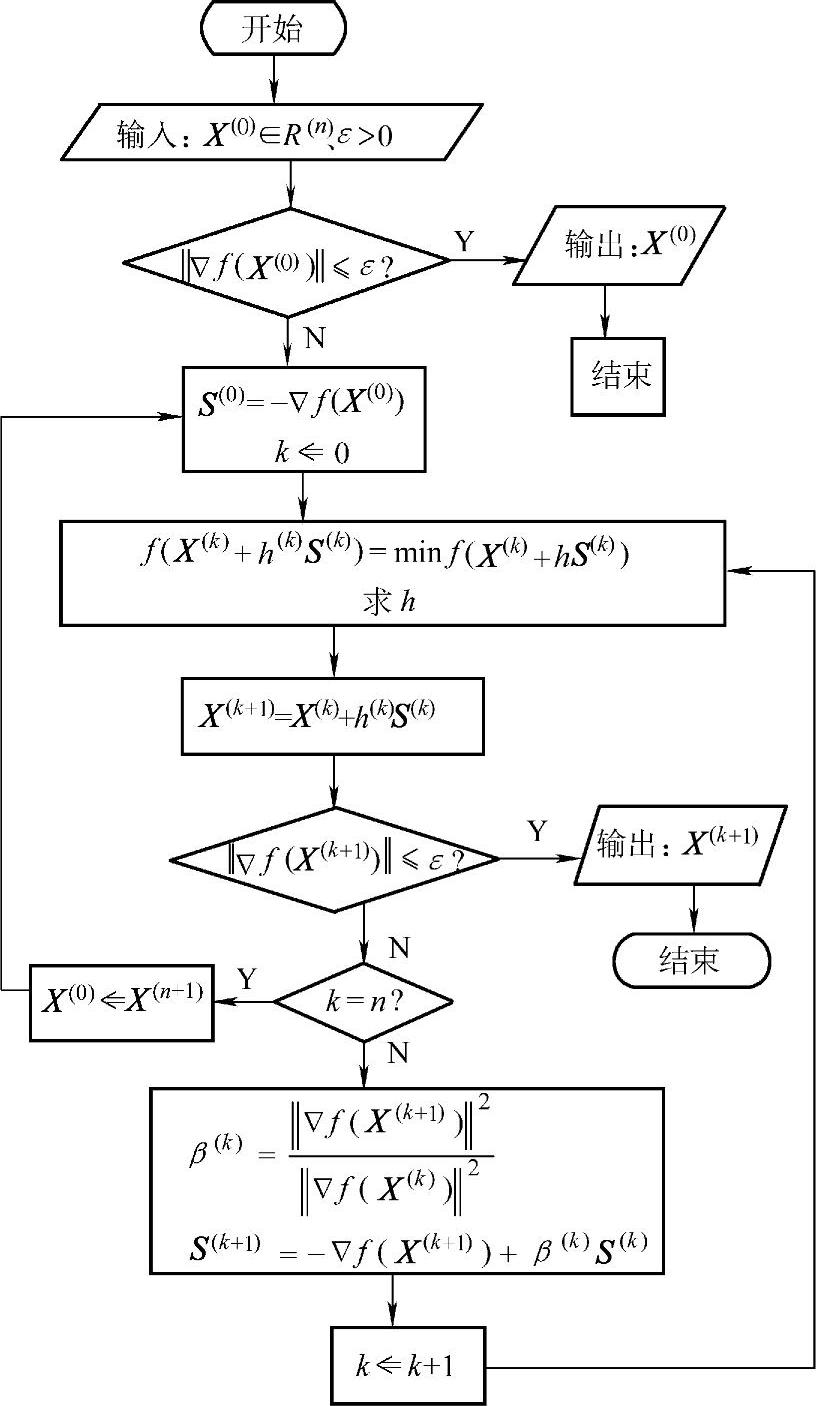
图4-4 共轭梯度法程序框图
解 给定初始点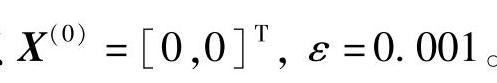
因为在初始点处的梯度
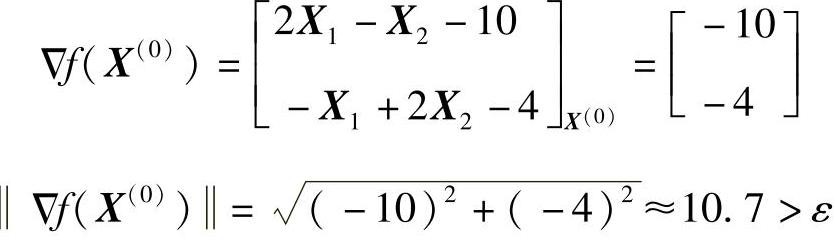
所以进行迭代计算。(www.daowen.com)
第一次迭代计算:
取 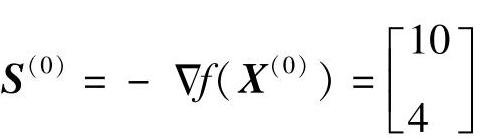
利用一维搜索,求得h(0)≈0.763157894,则
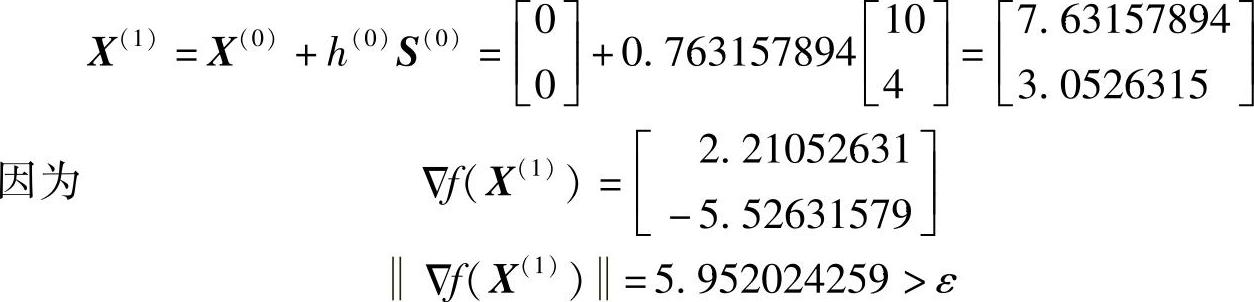
所以进行下一次迭代。
第二次迭代计算:
因为k=1<n=2,所以计算β(0):
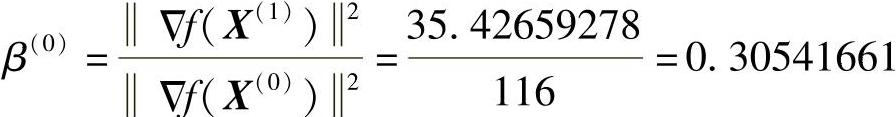
取 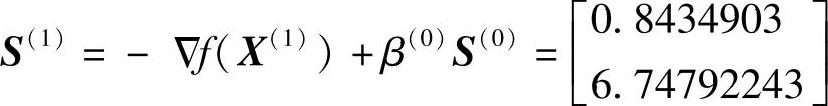
然后利用一维搜索求得h(1)=0.436781609,则
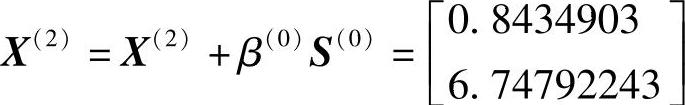
检验是否满足收敛准则,即
因 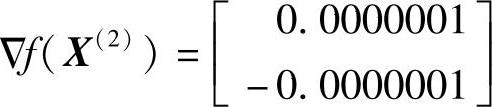
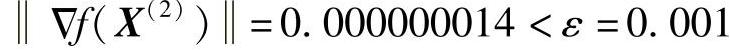
达到精度要求,故停止迭代计算,结果为
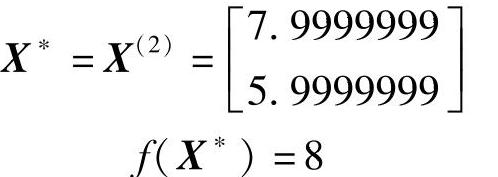
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关压力容器优化设计的文章







