如何用梯度法求函数f的极小值和极小点

梯度法的迭代计算步骤如下：

1）给定X^（0）∈E^*，ε＞0，置0⇒k。

2）计算Δf（X^（k））。

3）检验是否满足条件：|Δf（X^（k））|≤ε，若满足，迭代停止，X^*=X^（k）；否则进行4）。

4）求h^（k）∈E¹，使其满足条件：

5）返回进行2）。

梯度法的迭代过程如图4-2所示。

【例4-1】试用梯度法求f（X）=x²₁+5x²₂+6的极小点和极小值。

解 设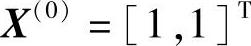，f（X^（0））=12，ε=0.01。

第一次迭代计算：

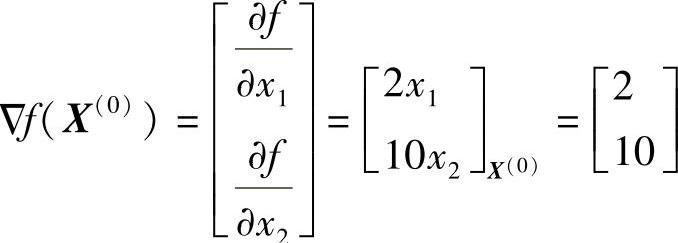
求h^（0）：

图4-2 梯度法程序框图

解得h^（0）=0.103

则

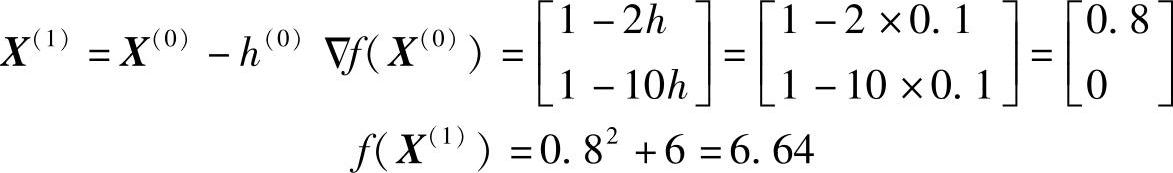
因为

故需继续进行迭代计算。

第二次迭代计算：

第二次迭代计算后得到：

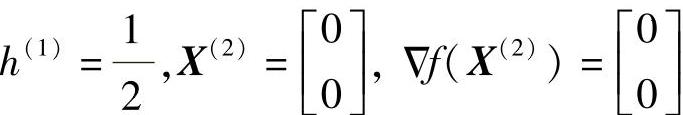
因为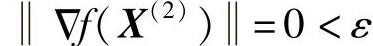

所以最后结果为(https://www.daowen.com)

f（X^*）=f（X^（2））=6

【例4-2】 用梯度法求目标函数f（X）=x²₁+25x²₂的最优解。初始点取为X^（0）=[2，2]^T，迭代精度ε=0.005。

解 函数的梯度

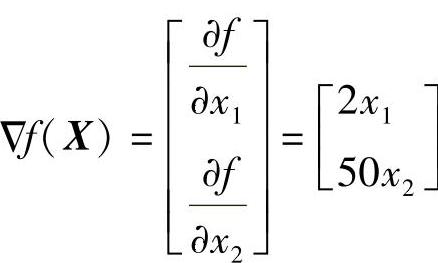
第一次迭代：

因为

f（X^（0））=104

故沿X（0）点的负梯度方向作一维搜索

设 f（h）=（2-4h）2+25（2-100h）2

令f′（h）=0，求得一维搜索的最优步长h^（0）=0.02003072，得迭代点、函数值及梯度值为

以下各次迭代过程同上，计算结果列于表4-1中。

表4-1 各次迭代计算结果

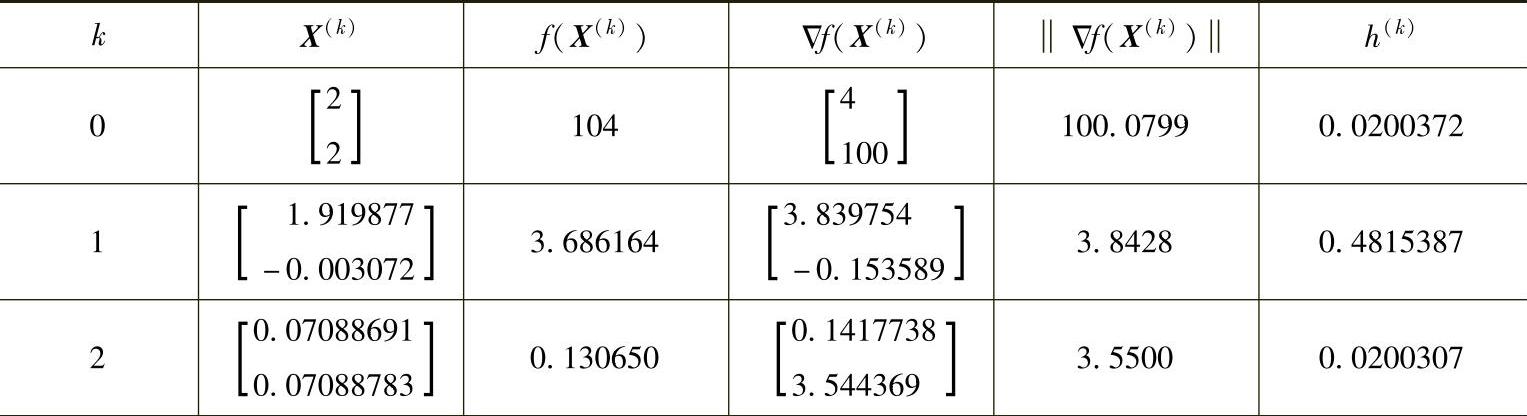
（续）

经过第五次迭代后，得Δf（X（5））=0.0049＜ε=0.005，得最优解为

f（X^*）=0.000006

本题的搜索图形如图4-3所示。

梯度法的优点是：简单；每次迭代工作量小，要求的存储量也小；对初始点要求不严格。缺点是：在极小点附近收敛慢；其收敛快慢受变量尺度影响较大；它对小扰动不太稳定。

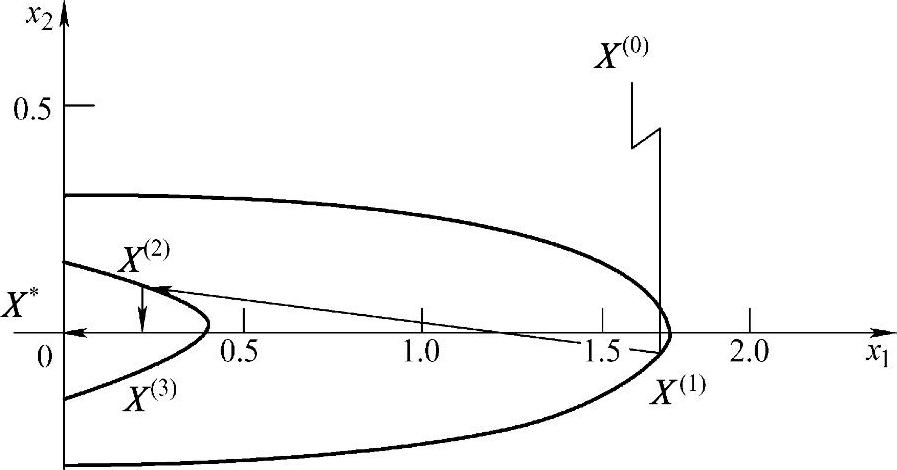
图4-3 例4-2的梯度法搜索图形