二次插值法又称抛物线法。它的基本思想是,用三个点的函数值来构成一个低次插值多项式,以近似地表达目标函数,并将这个多项式的极小点作为原函数极小值的近似值。它与切线法不同之处是:切线法利用一点的函数值和该点的一阶和二阶导数值来构造此二次函数,而二次插值法则利用三个点的函数值来构造。
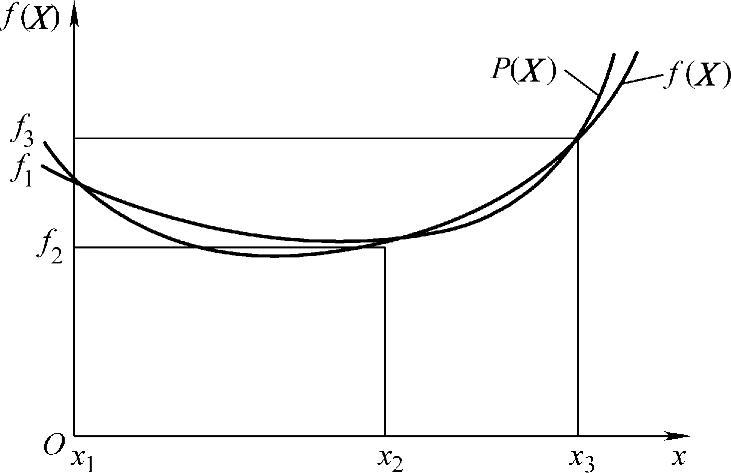
图3-13 二次插值法图解
如图3-13所示,假定目标函数f(X)在三个点(x1<x2<x3)的函数值分别为
f1,f2和f3,且f2<f1,f2<f3。设
P(X)=a0+a1X+a2X2 (3-11)
为所需的插值多项式,它应满足条件:
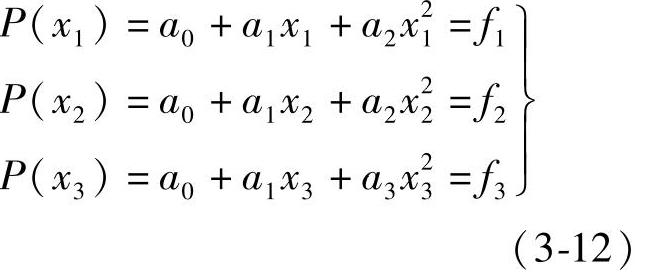
对多项式(3-11)求导数并令其值为零,得
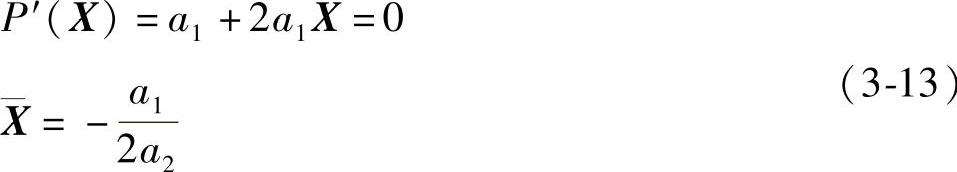
式(3-13)为计算近似极小点公式。为此,需求出a0和a2。由方程组(3-12),得
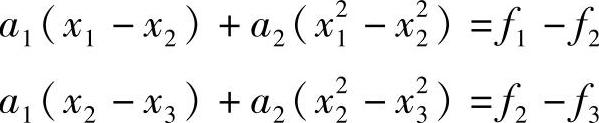
解此方程组,得
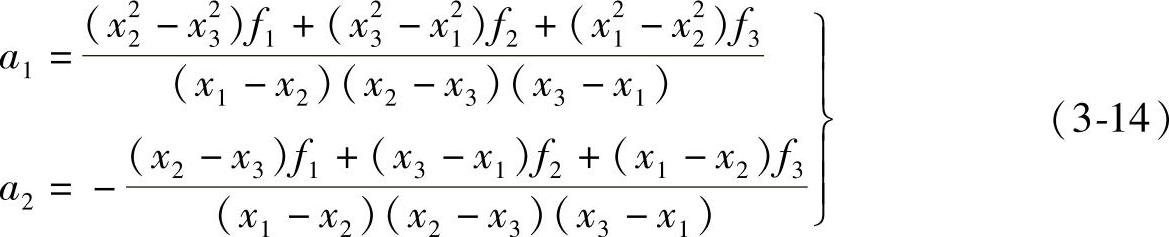
代入式(3-13),得极值点公式:
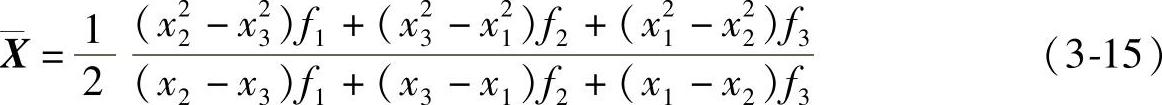
X即为f(X)的极小点的新的近似点,若|x2-X|<ε,则X即可视为f(X)在[x1,x3]上的近似最优解;否则缩小区间(去掉其中函数值最大者,构成新的三点,但应保持函数值两头大、中间小的性质),继续进行迭代计算,直至满足|x2-X|<ε为止。
二次插值法的迭代过程如图3-14所示。(https://www.daowen.com)
【例3-6】 试用二次插值法求解函数f(X)=x2-10x+36的极小值。
解 给定初始区间[X(1),X(3)]=[0,10],允许误差ε=0.01。
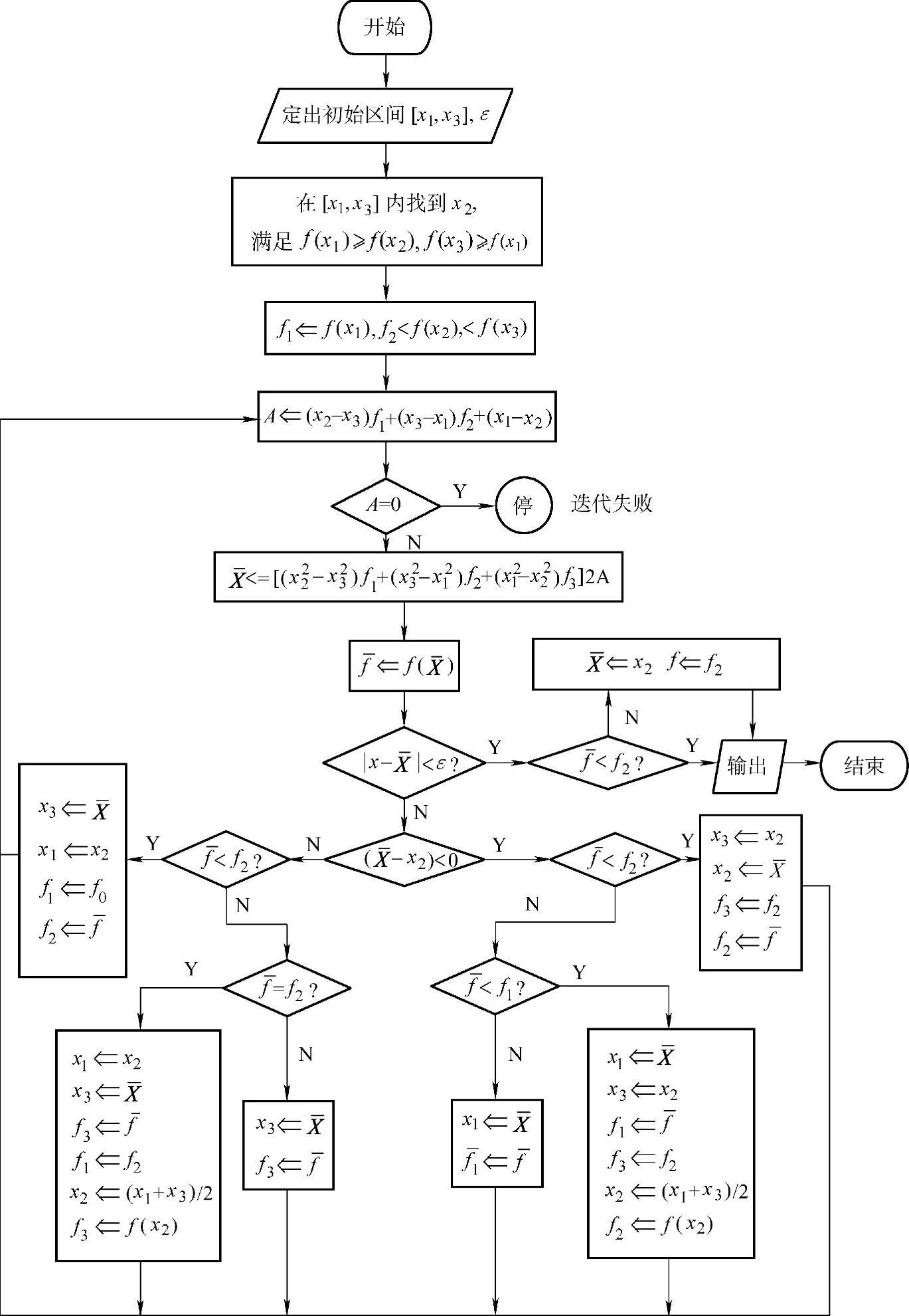
图3-14 二次插值法程序框图
第一次选代计算:
f1=f(X(1))=0-10×0+36=36
f3=f(X(3))=102-10×10+36=36
取X(2)=8,则
f2=f(X(2))=82-10×8+36=20
利用式(3-13)计算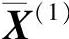 ,得
,得
X(1)=5
于是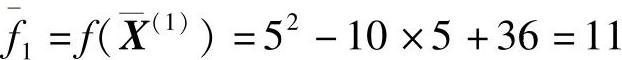
第二次迭代计算:
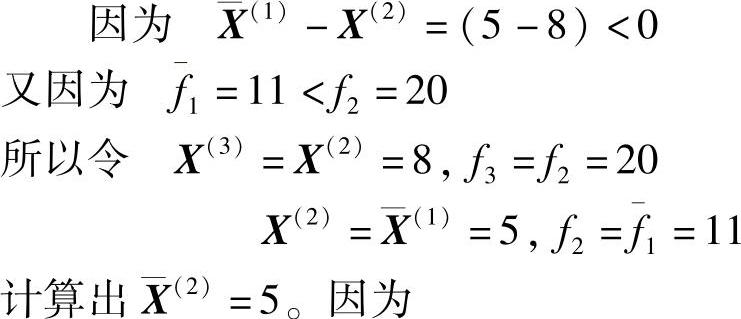
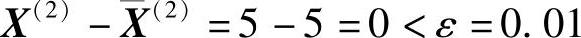
所以,计算结果为
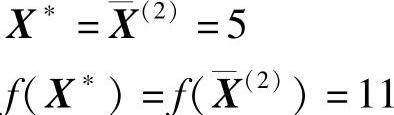
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






