当目标函数f（X^（k）+h^（k）S^（k））存在一阶连续导数，且二阶导数f″（X^（k）+h^（k）S^k）＞0时，可用切线法求方程f′（X^（k）+h^（k）S^k）=0的根，此根即为最优化步长因子h^*。

切线法即牛顿（Newton）法，其原理如图3-11所示。设在曲线y=f′（X）上，k点的切线与x轴的交点为X^（k+1），由几何关系得斜率

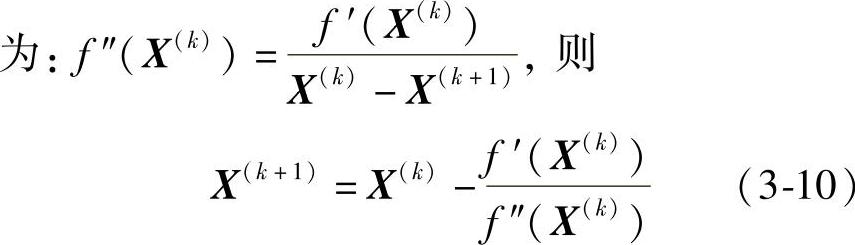
上式可作为求解f′（X）=0的迭代公式。可以证明，当k足够大时，总可以满足：

X^（k）-X^（k-1）≤δ或|f′（X^（k））|≤ε则认为X^（k）是最优点X^*的近似值。式中δ和ε是给定的允许误差，且δ和ε均大于0。

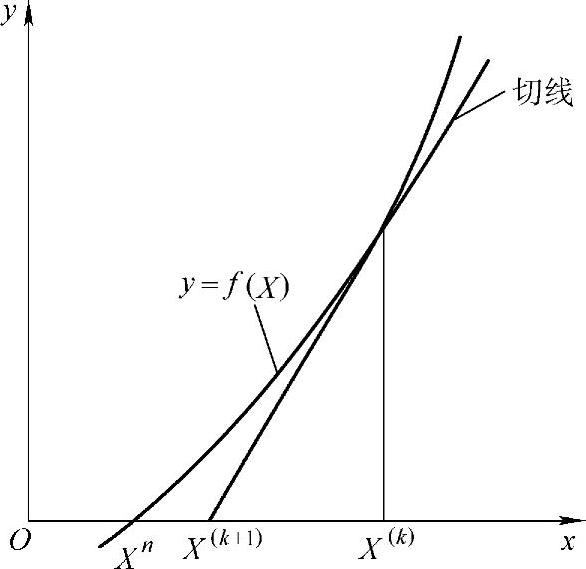
图3-11 切线法原理示意图

切线法最大的优点是收敛得快，但对于所有的X，当条件f″（X）≥0不能满足时，在迭代过程中会引起发散。切线法的迭代计算过程，如图3-12所示。

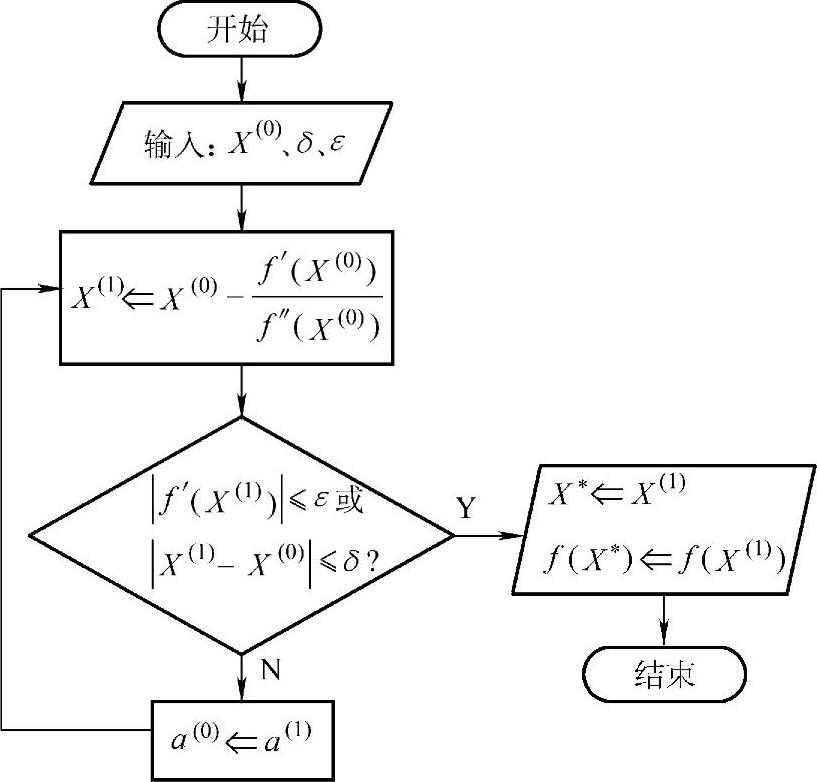
图3-12 切线法程序框图

【例3-5】试用切线法求函数f（X）=x²-10x+36的极小点。

解 设初始点X（0）=0，允许精度ε=0.01。

第一次迭代计算：(www.daowen.com)

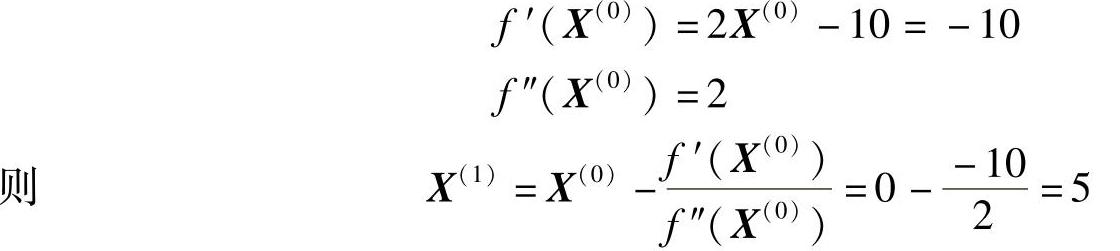
第二次迭代计算：

令X^（1）=X^（0）=5，则

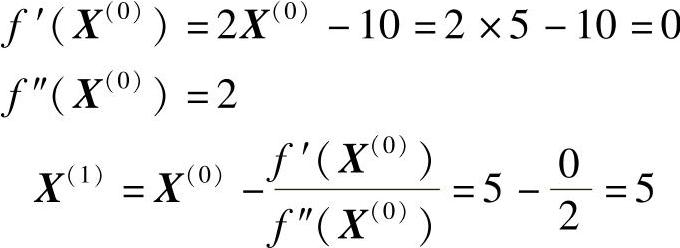
则

因为 |X^（1）-X^（0）|=|5-5|=0＜ε=0.01

故停止迭代，获得结果为

X^*=X^（1）=5

f（X^*）=5²-10×5+36=11

该题的BASIC语言程序（程序中，X0=X^（0），E=ε）如下：