黄金分割法又称0.618法，是一种消去法。消去法的基本原理是，在搜索区间内任取两点，计算其函数值并加以比较，舍去较大值所在区部分（图3-5），把搜索区间缩小，直至最小点存在的范围达到允许的误差范围为止。

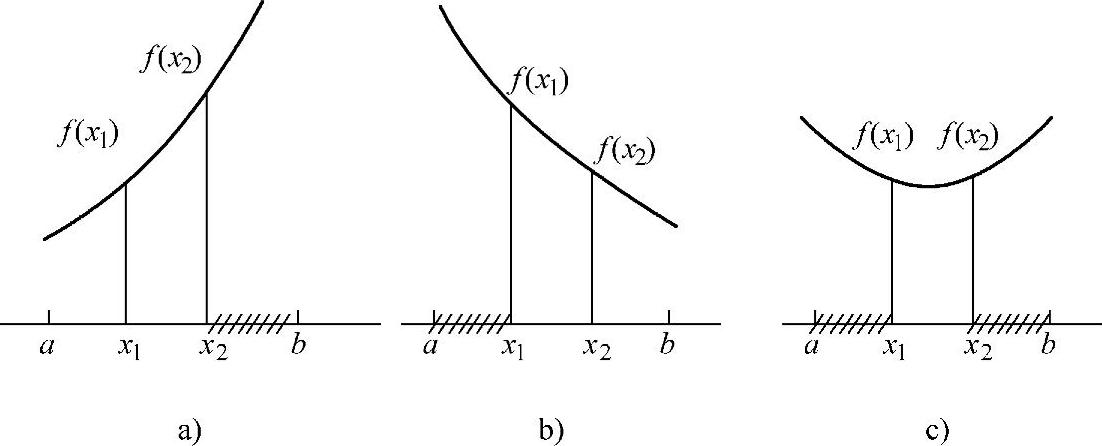
图3-5 消去法原理图解

黄金分割是将一条长为L的线分为两段，较长的一段记为C，较短的一段记为（L-C），L、C、（L-C）三者间应满足如下关系（图3-6）：

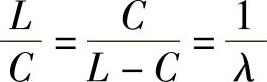
式中 λ——比例常数。

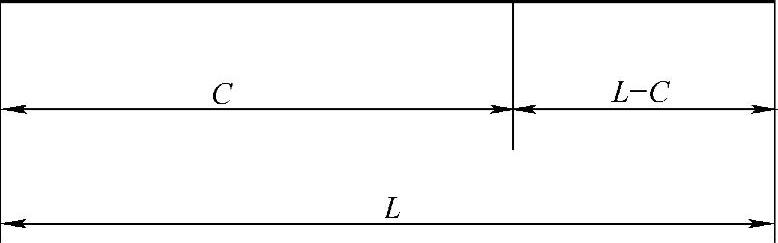
图3-6 L与C的关系

由上式得

C²+LC-L²=0

或

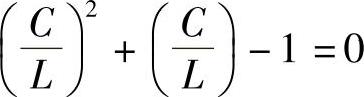
令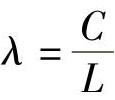，则上式写成：

λ²+λ-1=0

解得两根，取其正根：

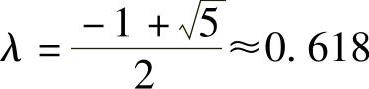
于是 C=λL≈0.618L

即黄金分割点（长段）位于0.618L处，而短段则为L的0.382倍。黄金分割法适用于[a，b]区间上的任何单峰函数求极小值问题。如图3-7所示，x₁、x₂的选取应保证如下关系成立：

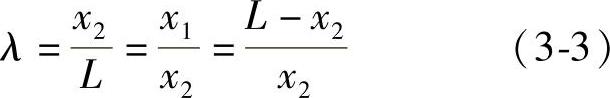
黄金分割法的具体计算方法及步骤如下：

1）给定区间[a，b]（a＜b）及允许误差ε＞0。

2）置a+0.618（b-a）⇒x₂，a+0.382（b-a）⇒x₁。

3）计算f（x₁）及f（x₂）之值，并置f（x₁）⇒f₁，f（x₂）⇒f₂。

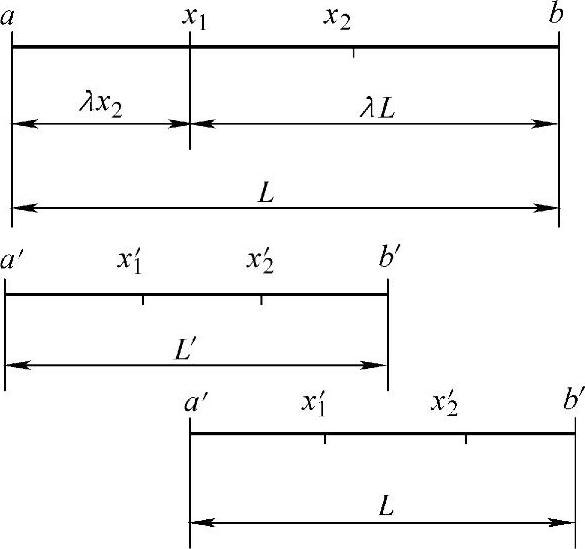
图3-7 黄金分割法示意

4）检验是否满足收敛性判别准则b-a≤ε，若满足，则进行5），否则进行6）。

5）比较是否满足不等式f₂＞f₁，若满足，则输出x₁，f₁为近似最优解，否则输出x₂，f₂为近似最优解，停止迭代。

6）若f₂＞f₁，则置x₂⇒b，x₁⇒x₂，a+b-x₂⇒x₁，f₁⇒f₂，f（x₁）⇒f₁，返回进行4）；否则x₁⇒a，x₂⇒x₁，a+b-x₁⇒x₂，f₂⇒f₁，f（x₂）⇒f₂，返回进行4）。(www.daowen.com)

黄金分割法的迭代过程如图3-8所示。

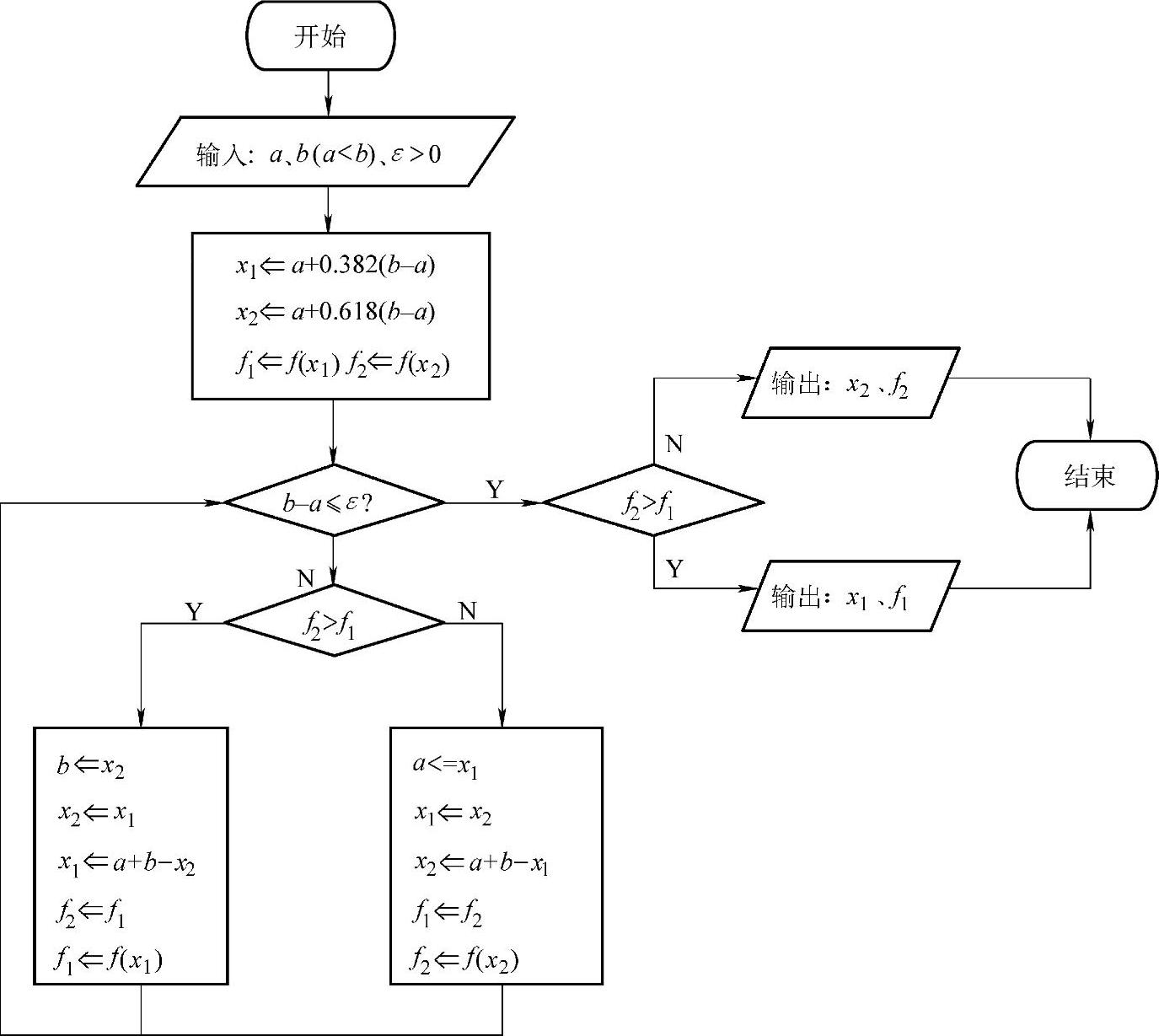
图3-8 黄金分割法程序框图

【例3-3】 试用黄金分割法求函数f（X）=（x-3）2的最优解。已知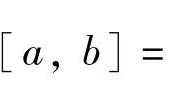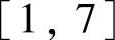，取ε=0.4。

解（1）取内分点并计算函数值

x₁=a+0.382（b-a）=3.292

x₂=a+0.618（b-a）=4.708

y₁=f（x₁）=0.085264

y₂=f（x₂）=2.917264

（2）缩短区间 因有y₁＜y₂，故作如下置换与计算：

b⇐x₂=4.708，x₂⇐x₁=3.292

y₂⇐y₁=0.085264

x₁=a+0.382（b-a）=2.416456

y₁=f（x₁）=0.340524

（3）检验是否满足收敛准则

b-a=4.708-1=3.708＞ε

条件不满足，返回（2），进一步缩短区间。

各次循环迭代计算结果见表3-1。

循环到第7次时，因为

b-a=3.085305-2.750914=0.334391＜ε

故迭代可结束，结果为

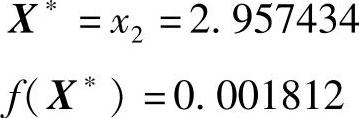
表3-1 例3-3的各次迭代结果

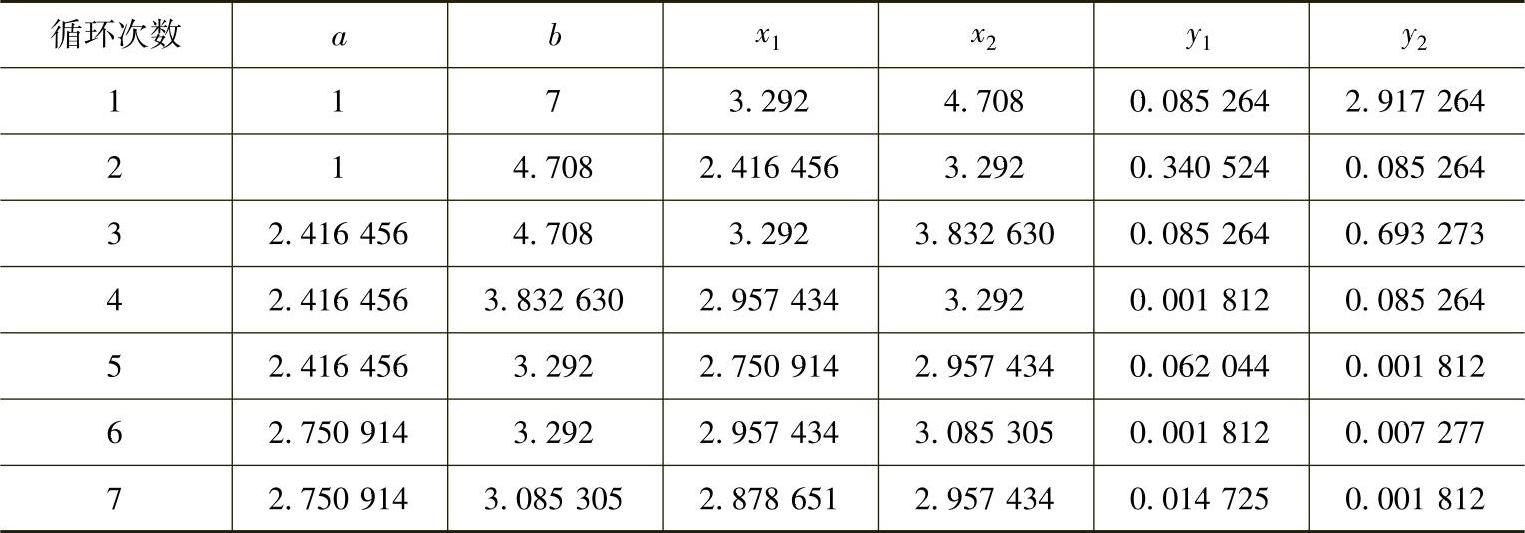
当迭代到第k次时，若满足0.618^k（b-a）≤ε，亦可将最终区间的中点及其函数值作为最优解输出：