初始搜索区间[a，b]确定之后，一维优化的任务就在于通过某种方法将此区间逐步缩小到最优点X^*附近极小的邻域内。该邻域的大小取决于计算者根据实际问题的需要而预定的收敛精度ε（ε＞0），或称迭代精度。

格点法是一种应用序列消去法原理的直接寻优法。其具体思路是：设函数f（X）的初始搜索区间为[a，b]，在此区间内取n个内等分点x₁，x₂，…，x_n，并计算这些点的函数值，记作y₁，y₂，…，y_n，比较这些函数值的大小，找出其中的最小者：

y_m=min{y_i，i=1，2，…，n}于是在与y_m相对应的点x_m之左右相邻点x_m-1和x_m+1之间即构成了包含f（X）极小点X^*在内的被缩短了的新区间，如图3-3所示。

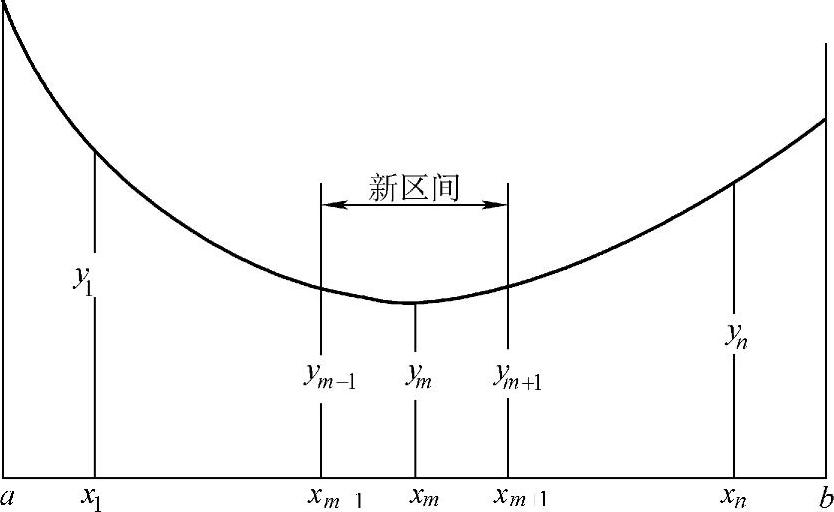
图3-3 格点法图解

如果新区间的长度还不能满足预定的精度要求，则将其作为新的初始区间，重复上述步骤，进一步缩短区间，直到满足x_m+1-x_m-1≤ε时，x_m和y_m就是具有足够精度的一维优化近似解：X^*=x_m，Y^*=y_m。

在一维搜索中，每一次区间缩短的快慢程度可用新旧区间长度之比来表示，称为区间缩短率，常用λ表示。在格点法中，若每次区间缩短时取内分点数为n，依定义，则有

由此可见，内分点数取得越多，λ值越小，意味着区间缩短得越快。但另一方面，寻优过程也越长，越费机时。因而n不宜取过大。

格点法的一维优化过程如图3-4所示。

【例3-2】 试用格点法求一维目标函数f（X）=4x²-12x+10的最优解。已知初始区间[a，b]=[1，2.2]，迭代精度ε=0.2，n=4。

解 初始区间端点的函数值为

f（a）=2，f（b）=2.96

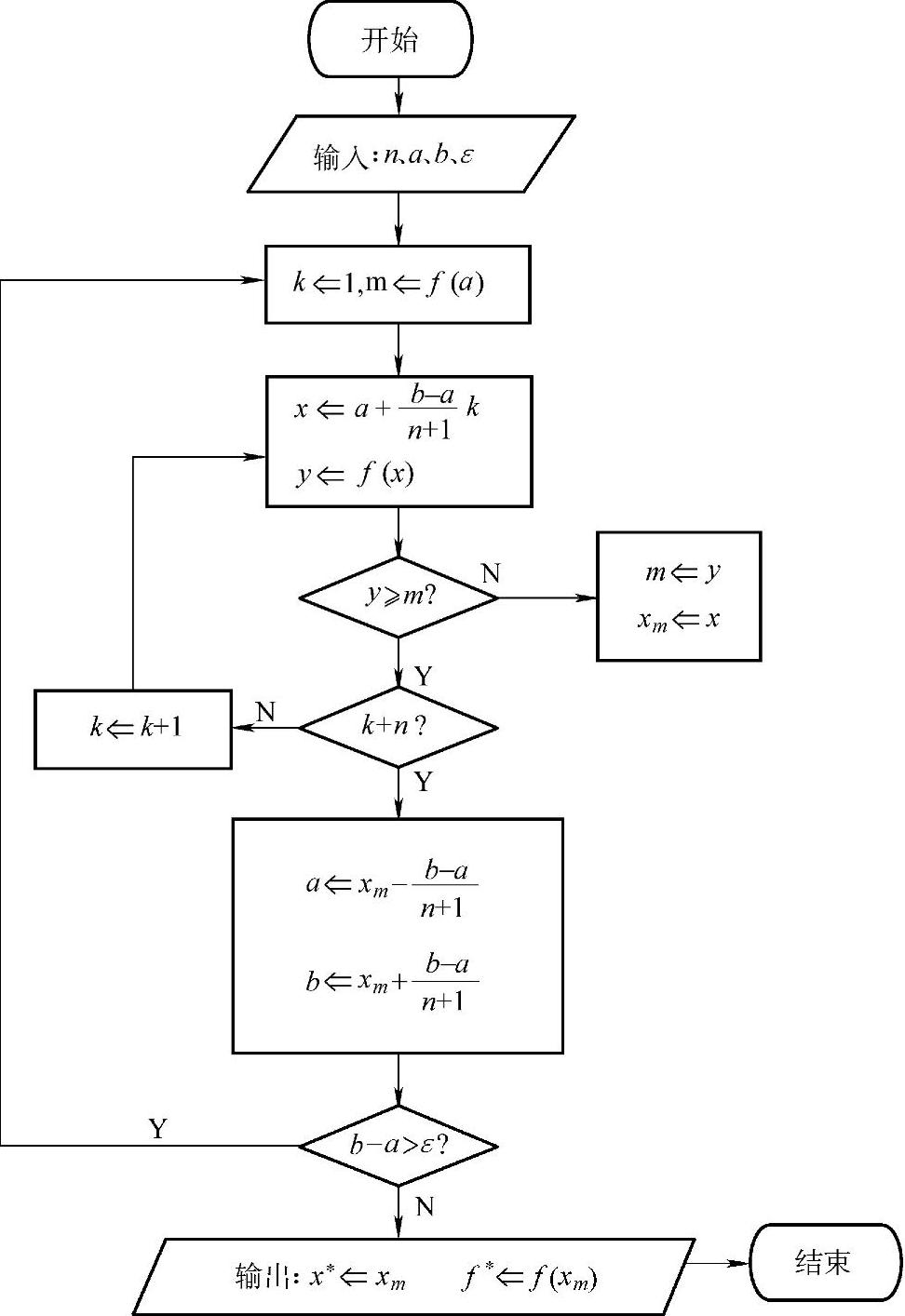
图3-4 格点法程序框图(www.daowen.com)

区间中内分点的位置及其函数值按下式计算：

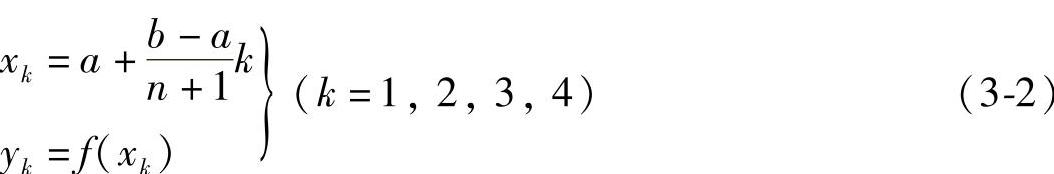
（1）第一次计算 把已知条件代入式（3-2），分别计算x_k和y_k：

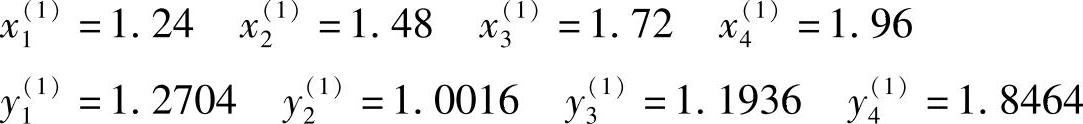
显然，最小函数值：

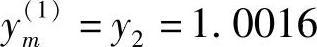
对应的点为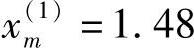，新区间的端点是

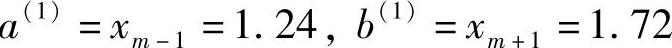
但 b（1）-a（1）=0.48＞ε=0.2

未满足迭代精度，需继续进行计算。

（2）第二次计算 以新区间取代旧区间，重复上述步骤，结果如下：

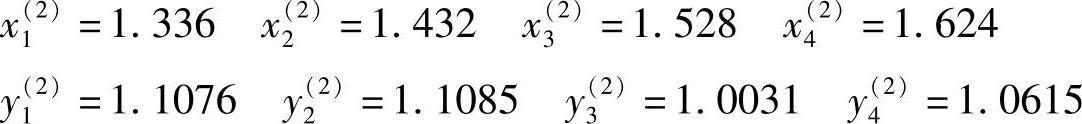
于是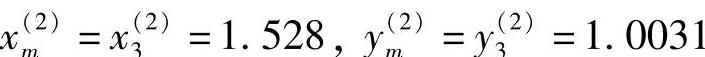，，新区间端点为：a（2）=1.432，b（2）=1.624。因为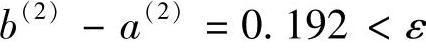，故其最优解为：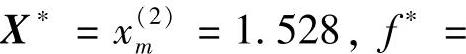

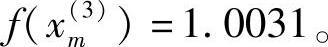
从上述优化过程可以看出，格点法的计算程序简单。对于离散变量的一维优化问题，分点可以取在这些离散值处。不足之处是，格点法的计算效率较低，即在一定精度要求下计算函数值的次数较多，因而不宜用于维数较高的复杂问题中。