【摘要】:x3x1,y3y1x1x2,y1y2,x2x3,y2y3注意,此处的x3仅作为倒换数据的暂用单元。2)y2>y3,如图3-1c中所示实曲线Ⅰ所示,则应继续作后退运算。先作如下置换:x1x2,y1y2x2x3,y2y3倍增进退距h2h后计算新点x3及其函数值:x3x2+h,y3=f重复上述过程,直至出现三点函数值依次为大—小—大时,取其左右两端点为初始搜索区间[a,b]。
进退距取负值,即h⇐-h0,置换点号使它自右向左反向排列,如图3-1c所示。
x3⇐x1,y3⇐y1
x1⇐x2,y1⇐y2,
x2⇐x3,y2⇐y3
注意,此处的x3仅作为倒换数据的暂用单元。将进退距加倍(h⇐2h)后,计算第三个后退点:
x3⇐x2+h,y3=f(x3)
比较函数值y2和y3的大小,可能也有两种情况:
1)y2<y3,如图3-1c中所示虚曲线Ⅱ所示,则初始区间即被确定a⇐x3,b⇐x1。
2)y2>y3,如图3-1c中所示实曲线Ⅰ所示,则应继续作后退运算。先作如下置换:
x1⇐x2,y1⇐y2
x2⇐x3,y2⇐y3倍增进退距h⇐2h后计算新点x3及其函数值:
x3⇐x2+h,y3=f(x3)
重复上述过程,直至出现三点函数值依次为大—小—大时,取其左右两端点为初始搜索区间[a,b]。
进退法确定初始搜索区间的过程如图3-2所示。
【例3-1】 试用进退法确定函数f(X)=x2-6x+9的一维优化初始搜索区间[a,b]。设初始点x1=0,初始进退距h0=1。(www.daowen.com)
解 按图3-2流程,计算过程如下:
h=h0=1,x2=x1+h=1
y1=f(x1)=9,y2=f(x2)=4
因为,y2<y1,故作前进运算:
h⇐2h=2,x3=x2+h=3
y3=f(x3)=0
比较y2和y3,有y2>y3,再作前进运算:
x1⇐x2=1,y1⇐y2=4
x2⇐x3=3,y2⇐y3=0
h⇐2h=4,x3=x2+h=7
y3=f(x3)=16
再比较y2和y3,有y2<y3,故可令a⇐x1=1,b⇐x3=7,即初始搜索区间为[a,b]=[1,7]。
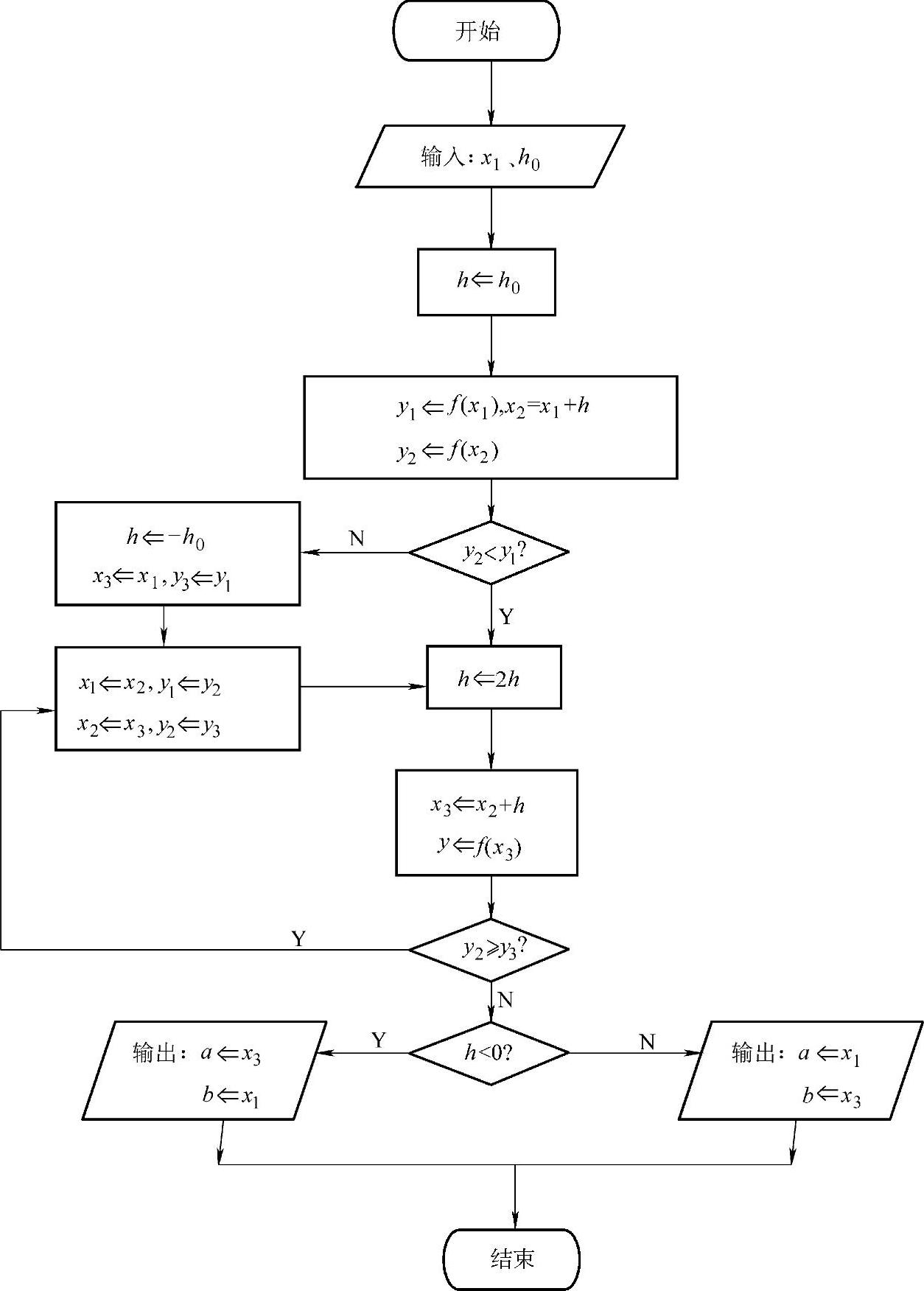
图3-2 进退法确定初始搜索区间程序框图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关压力容器优化设计的文章






