所谓满足可行性条件，是指沿该方向一定有可行点存在。即由X（k）点出发，沿S（k）方向，取适当步长h（k），则

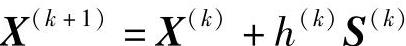
必须在可行域内。换言之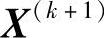，必须是可行点。其判断准则是：若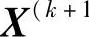）点的所有约束函数值都大于零，则它是可行域内部的可行点；若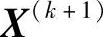点的某个或某几个约束函数值等于或接近于零，则该点是边界上的可行点，而这一个或几个约束称为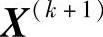点的起作用约束。对于在某一约束g_j（X）边界上的可行点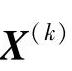，其满足可行性要求的搜索方向S^（k），一定是指向该起作用约束函数值的增大方向。若引用方向导数概念，则g_j（X）沿S^（k）的方向导数应大于零或等于零（当g_j（X）为线性函数时）。即

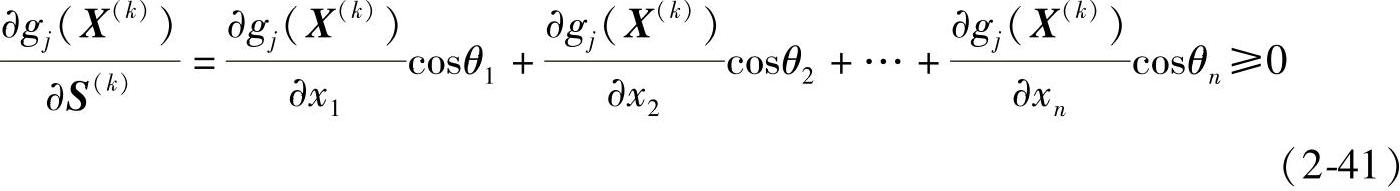
同理，若取搜索方向为单位矢量，则上式可用矩阵形式表示：

若以β_k表示矢量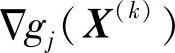与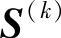的夹角，则有

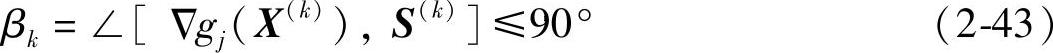
这表明，为满足可行性要求，搜索矢量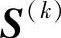与起作用约束函数梯度矢量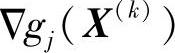的夹角应为锐角，其几何意义如图2-11a所示。(www.daowen.com)

如果迭代点X^（k）是在J个约束边界的相交处，则这些约束都是起作用约束，即

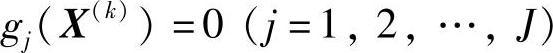
于是式（2-42）可改写成：

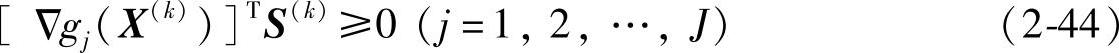
式（2-44）表明，为满足可行性要求，搜索矢量S^（k）应分别与J个起作用的约束梯度矢量Δg_j（X^（k））=0（j=1，2，…，J）的夹角均为锐角。图2-11b表示了迭代点X^（k）在两个约束边界交汇处的情况。对于约束g₁（X），可行方向应在过X^（k）点g₁（X）曲线的切线t₁-t₁的上方，对于g₂（X），可行方向又应在t₂-t₂的右上方，从而形成一个公共区域ξ。按前所述，搜索矢量S^（k）应限制在该区域内。

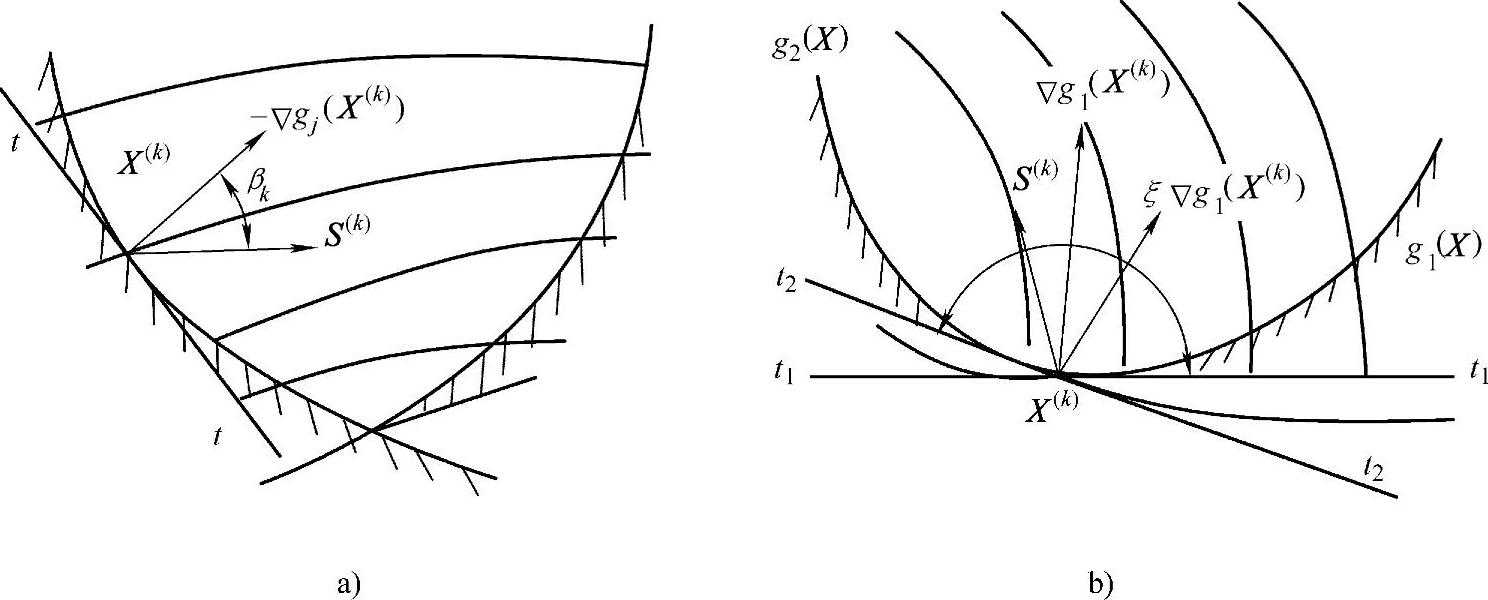
图2-11 可行性条件的几何意义