约束优化问题局部解二阶充分条件的优化方法

由2.3节知，无约束问题最优解的一阶必要条件是目标函数梯度在X点处为零向量，充分条件是f（X）在X点处的海赛矩阵为正定矩阵。而约束问题最优解的一阶必要条件是拉格朗日函数L（X，λ）在X点处的梯度为零向量。据此是否可以推测，L（X，λ）在X点处的海赛矩阵Δ²L（X，λ）为正定矩阵才能保证X是约束问题的最优点？

容易验证，上述条件是过强了。事实上，对于约束优化问题，变量X完全被限制于由约束函数所构成的可行域内，因而解X的极小性质也是在这个范围内而言的。所以，并没有理由一定要L（X，λ）在X处沿所有方向的二阶方向导数取正值，而应当仅要求它在X处沿起作用约束函数的方向τ上的二阶方向导数取正值。这里τ与约束函数梯度Δg_u（X）垂直，即＜τ，Δg_i（X）＞=0。

上述方向τ组成一维空间

综上所述，可建立约束优化问题解的二阶充分条件如下：

设函数f（X）和约束函数g_i（X）（i∈p∪q）具有连续的二阶偏导数，若存在着X∈Eⁿ满足下列条件：

1）K-T条件成立，即存在着乘子向量λ=（λ₁，λ₂，…，λ_p+q）^T，使得

且当i∈p时，λ_i和g_i（X）不同时为零。

2）对子空间M={τ|＜τ，Δg_i（X）＞=0，i∈m，m是X处的有效集}中的任意非零向量τ都有：

＜τ，Δ²L（X，λ）τ＞＞0

则X是约束优化问题的严格局部解（证明从略）。

【例2-6】 应用约束问题解的一阶必要条件和二阶充分条件，求解问题

Ω∶g（X）=x₂=0

解 该问题的拉格朗日函数为(https://www.daowen.com)

其梯度向量和海赛矩阵分别为

由前述知，问题的解必满足一阶必要条件：

ΔL（X，λ）=0

g（X）=0

即

解此方程组得唯一解：

x₁=0，x₂=0，λ=4

由此只有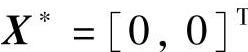可能是问题的解，相应的乘子为λ=4＞0，满足K-T条件。

为考察X是否为问题的解，我们验证它是否满足解的二阶充分条件。显然，在X处，约束X₂=0在X处的梯度向量为

这时，相应的子空间为

因此，对任意τ∈M，τ≠0，有

于是可知，X及λ满足解的二阶充分条件。也就是说，X=[0，0]^T是问题的唯一解，λ=4为相应的乘子。