1.起作用约束与不起作用约束

如前所述，一般的约束优化问题包含有不等式约束g_u（X）≥0（u=1，2，…，p）和等式约束h_v（X）=0（v=1，2，…，q），在可行设计点X^（k）处，若有g_u（X）=0，则该约束g_u（X）称为可行点X^（k）的起作用约束；而若g_u（X^（k））＞0，则该约束g_u（X）称为可行点X^（k）的不起作用约束。对于等式约束h_v（X）=0，显然在任一可行点处的等式约束都是起作用约束。

在可行点X^（k）处，起作用约束在X^（k）的邻域内起限制可行域的作用，而不起作用约束在X^（k）处的邻域内就不产生影响。因此应把注意力集中在起作用约束上。

2.IP型约束问题的最优解条件

图2-6所示为具有三个不等式约束的二维约束优化问题，分为以下三种情况。

1）最优点X^*在可行域内（见图2-6a）。在此情况下，X^*点的全部约束函数值g_u（X^*）＞0（u=1，2，3），即这组约束条件对其最优点X^*都不起作用。换言之，如果去掉全部约束，其最优点也仍是同一个X^*点。因此，这种约束优化问题与无约束优化问题是等价的。

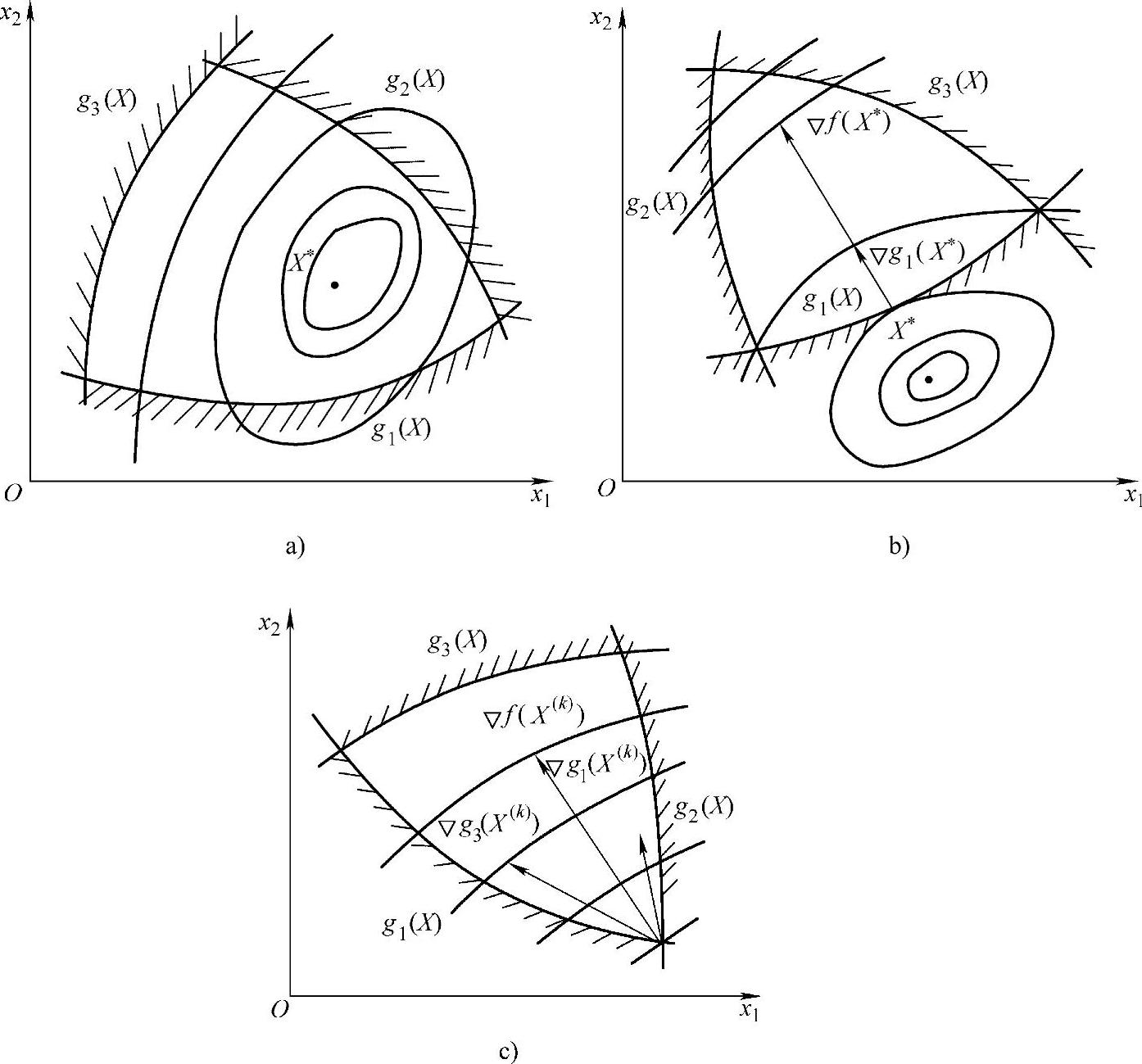
图2-6 二维不等式约束优化问题

2）约束最优点X^*位于g₁（X）的边界曲线与目标函数等值线的切点处（见图2_-6b）。此时g₁（X^*）=0，g₂（X^*）＞0，g₃（X^*）＞0。所以，起作用的约束仅为g₁（X）。既然X^*是f（X）等值线与g₁（X）边界线的切点，则对应的梯度矢量Δf（X^*）与Δg₁（X^*）必共线，且方向一致。若取非负乘子λ₁^*≥0，则在X^*处存在如下关系：

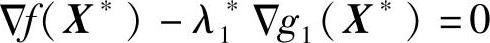
3）当前迭代点X^（k）在两约束的交点上（见图2-6c）。这时，Δf（X^（k））夹于Δg₁（X^（k））与Δg₂（X^（k））之间。显然，在X^（k）点处，起作用约束为g₁（X）和g₂（X）。在这种情况下，由于X^（k）点邻近的可行域内部不存在目标函数值比f（X^（k））更小的设计点，因而有：X^（k）=X^*。由图2-6c可知，此时X^（k）点的目标函数的梯度Δf（X^（k））可表达为约束函数梯度Δg₁（X^（k））和Δg₂（X^（k））的线性组合。若用X^*代替X^（k），则有

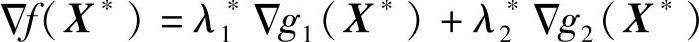
成立，且有λ₁^*≥0，λ₂^*≥0。

总结以上情况，对图2-6所示的二维约束优化问题，其最优解的一阶必要条件是

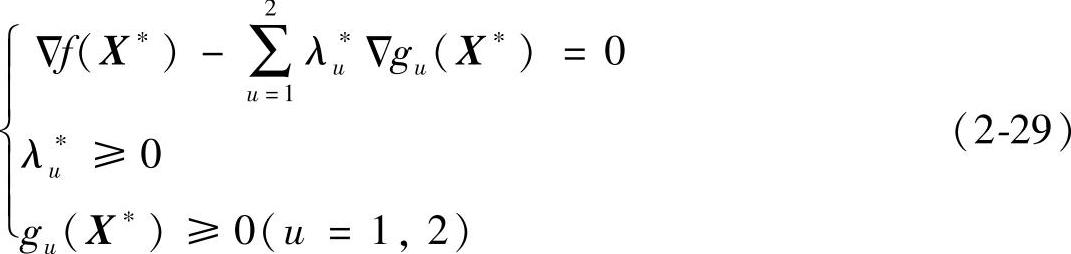
根据上面的分析，可归纳出IP型约束问题最优解的一阶必要条件如下：

设最优点X^*位于J个约束边界的汇交处，则J个约束条件组成一个起作用的约束集，对于X^*点，下式必成立：

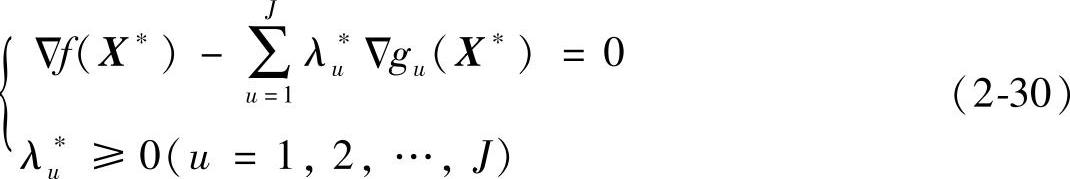
然而，在实际求解过程中，并不能预先知道最优点X^*位于哪一个或哪几个约束边界的汇交处。为此，把p个约束全部考虑进去，并取相应于不起作用约束的乘子λ_u^*为零，这样，上式可改写成：

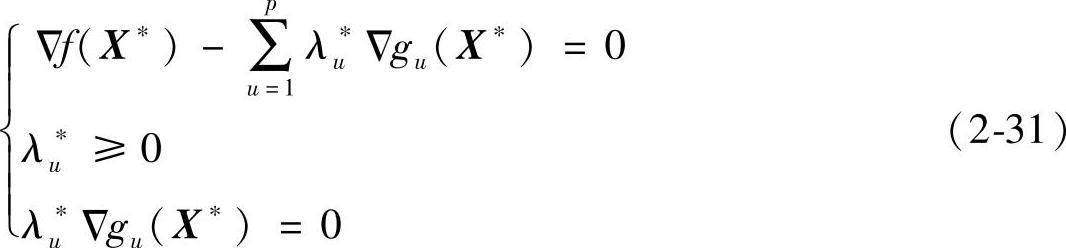
此即为IP型约束优化问题最优解一阶必要条件的一般表达式，它实际上等价于式（2-30）。这是因为，在X^*处，对于起作用约束，必有g_u（X^*）=0（u=1，2，…，J）；对于不起作用约束，尽管g_u（X^*）＞0，但λ_u=0。

3.EP型约束问题的最优解条件

图2-7所示为具有一个等式约束条件的二维优化问题，其数学模型为

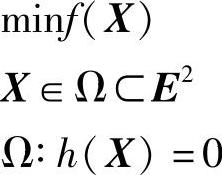
该问题中，等式约束曲线h（X）=0是它的可行域，而且目标函数等值线f（X）=C与h（X）=0的切点X^*是该约束问题的最优点。在X^*点处，目标函数的梯度Δf（X）与约束函数的梯度Δh（X^*）共线。因此，必定存在一个乘子μ^*，使得Δf（X^*）-μ^*Δh（X^*）=0成立。对于一般的n维等式约束优化问题：

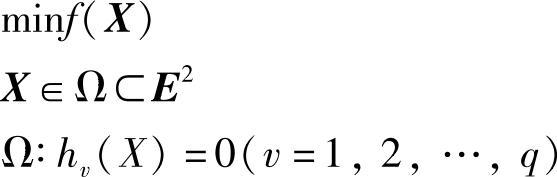
其最优解的一阶必要条件为

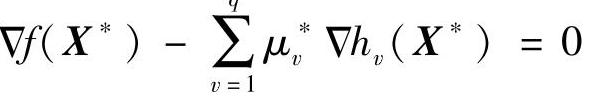
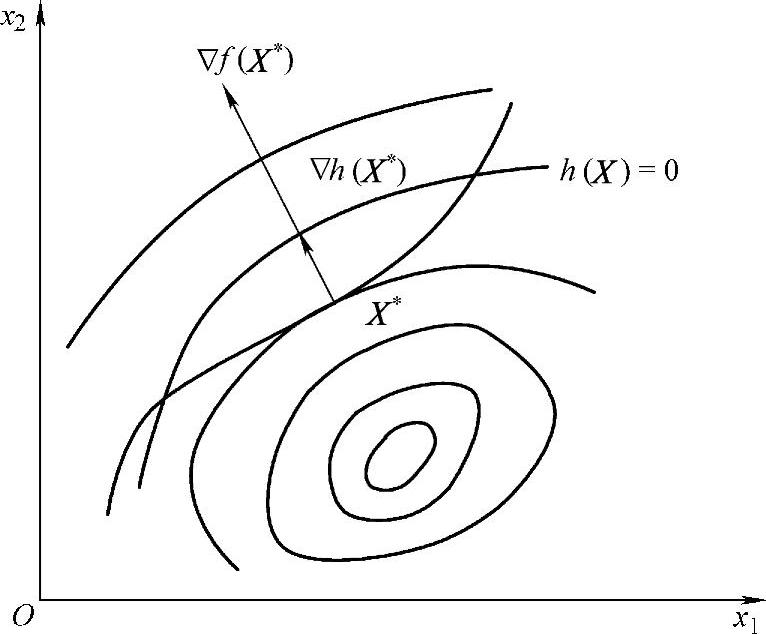
图2-7 二维等式约束优化问题

4.GP型约束问题的最优解条件

由上述IP型和EP型约束问题的最优解条件，可推出一般约束优化问题的一阶必要条件。设n维一般约束优化问题的数学模型为

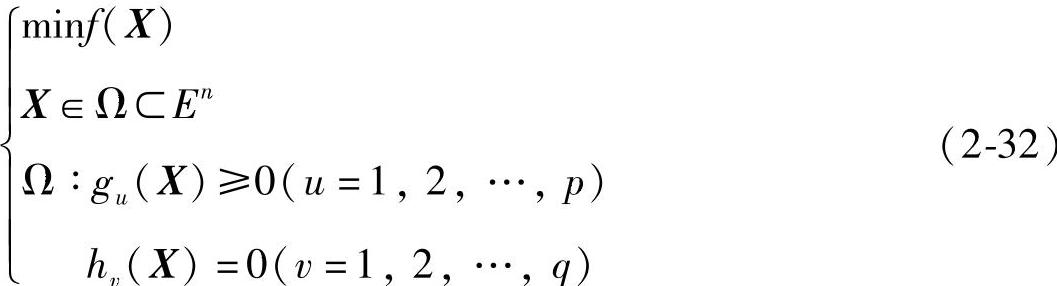
则X^*为其最优解的一阶必要条件应为

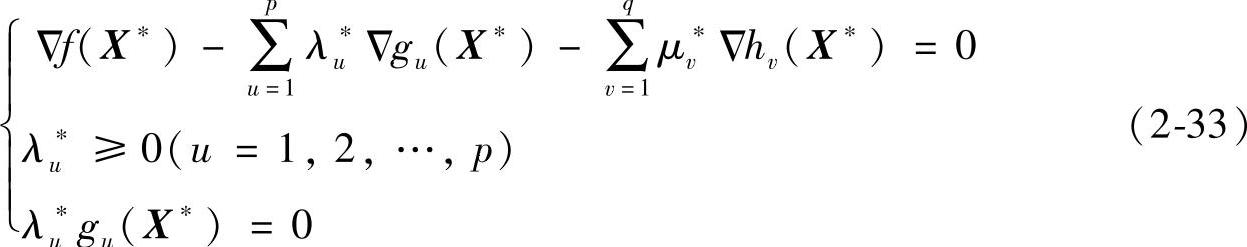
若令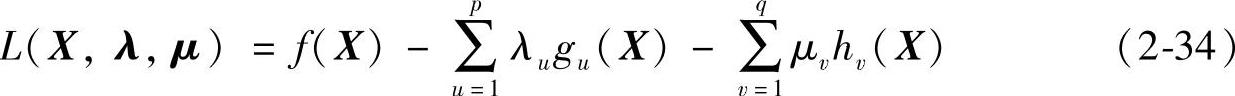

则称L（X，λ，μ）为关于问题（2-32）的广义拉格朗日（Lagrange）函数，式中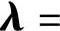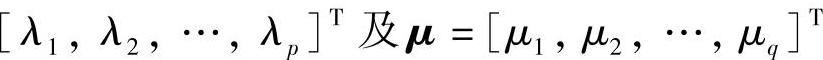，是拉格朗日乘子。(www.daowen.com)

于是，式（2-33）中第一式可写成：

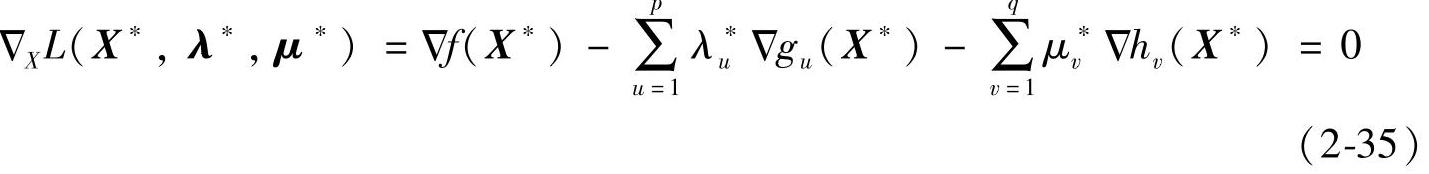
5.库恩-塔克（Kuhn-Tucker）条件

在实际优化计算中，常常需要判断某可行迭代点X^（k）是否可作为约束最优点X^*输出而结束迭代，或者检验所输出的可行结果是否已满足约束最优解的必要条件。这种判断或检查通常是借助于库恩-塔克条件（简称K-T条件）进行的。

K-T条件指出，点X^（k）要成为约束优化问题最优解的必要条件是：目标函数f（X）的负梯度-Δf（X^（k））可以表示为起作用约束函数梯度Δg_u（X^（k））和Δh_v（X^（k））的线性组合。即

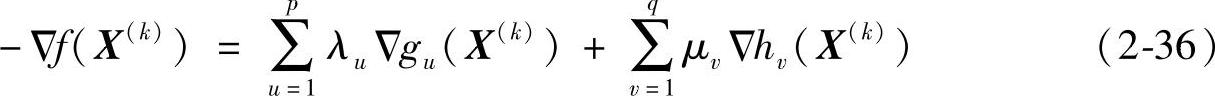
式中其他符号的意义同前。当不等式约束g_u（X^（k））≥0时，上式可写成：

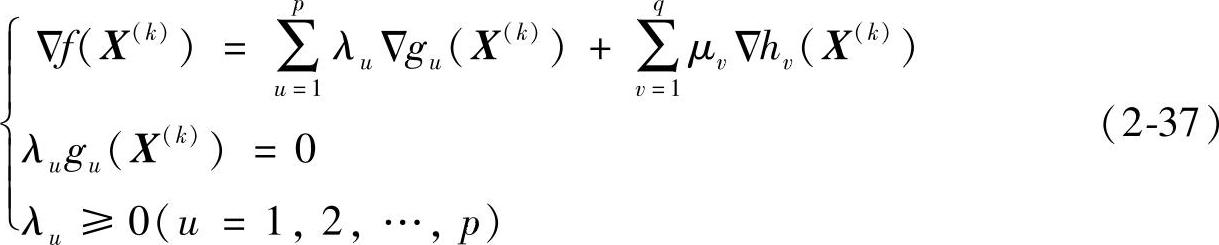
若引入广义拉格朗日函数及如下的向量：

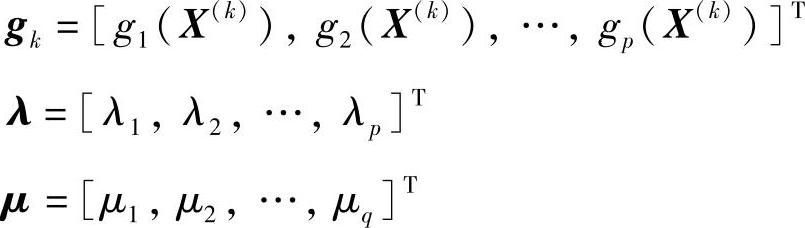
则式（2-37）可写成更紧凑形式：

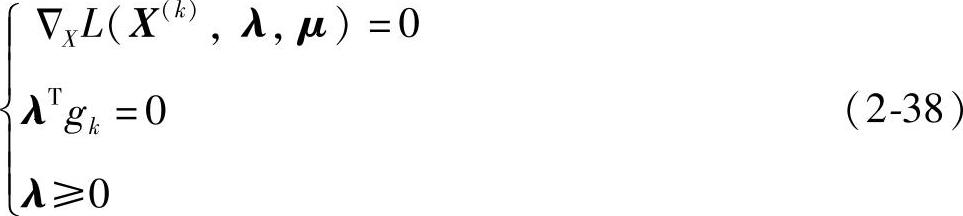
凡满足式（2-36）、（2-37）或（2-38）的迭代点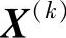即可以作为最优点输出。这时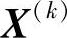，称为K-T点。

【例2-5】 设二维约束优化问题的数学模型为

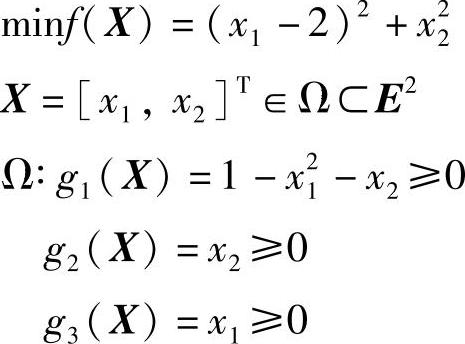
它的当前迭代点为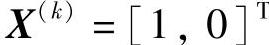，试用K-T条件判断其是否为约束最优点。

解（1）计算X（k）点的诸约束函数值

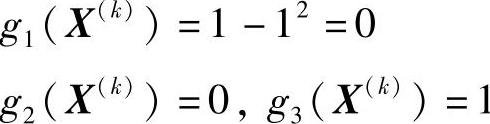
可知X^（k）点是可行点。

（2）X^（k）点起作用的约束

g₁（X）=1-x²₁-x₂=0

g₂（X）=x₂

（3）求X^（k）点的诸梯度

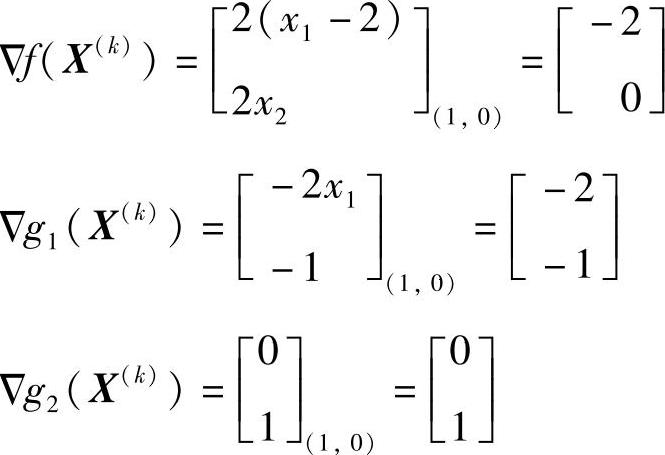
（4）求拉格朗日乘子 把以上计算结果代入式（2-37），可得

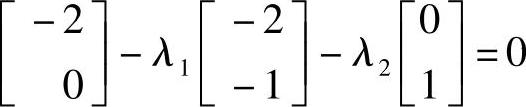
写成线性方程组

-2+2λ₁=0

λ₁^-λ2=0

解得：λ₁=λ₂=1＞0，满足K-T条件。所以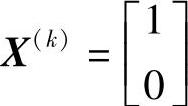，为约束局部最优点。而且，容易验证，f（X）是凸函数，可行域为凸集，故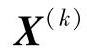也是该问题的全局最优解，如图2-8所示。

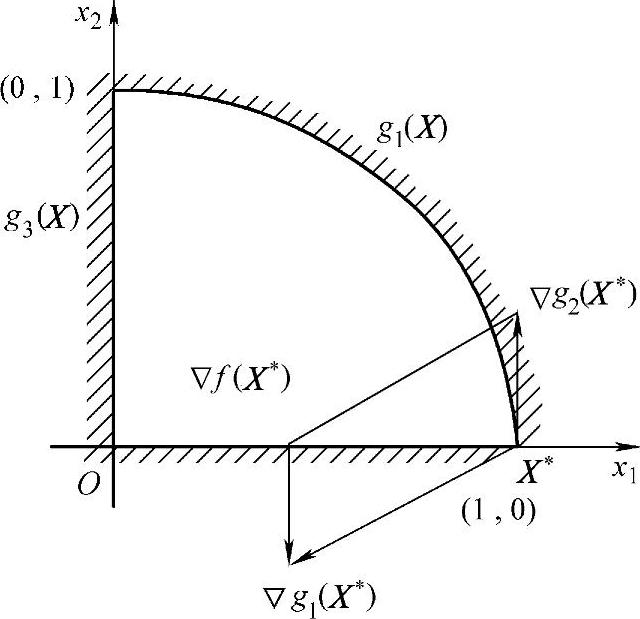
图2-8 例2-5约束优化问题图解

6.K-T条件的几何意义

K-T条件的几何意义如图2-9所示，起作用约束函数的梯度向量，在设计空间内构成一个锥体。若满足K-T条件，则目标函数的负梯度向量-Δf（X）应包含在此锥体之内。显然，图2-9a表示X并非目标函数的最优点，因为它不满足K-T条件；而图2-9b所示的X才是目标函数的一个局部最优点。

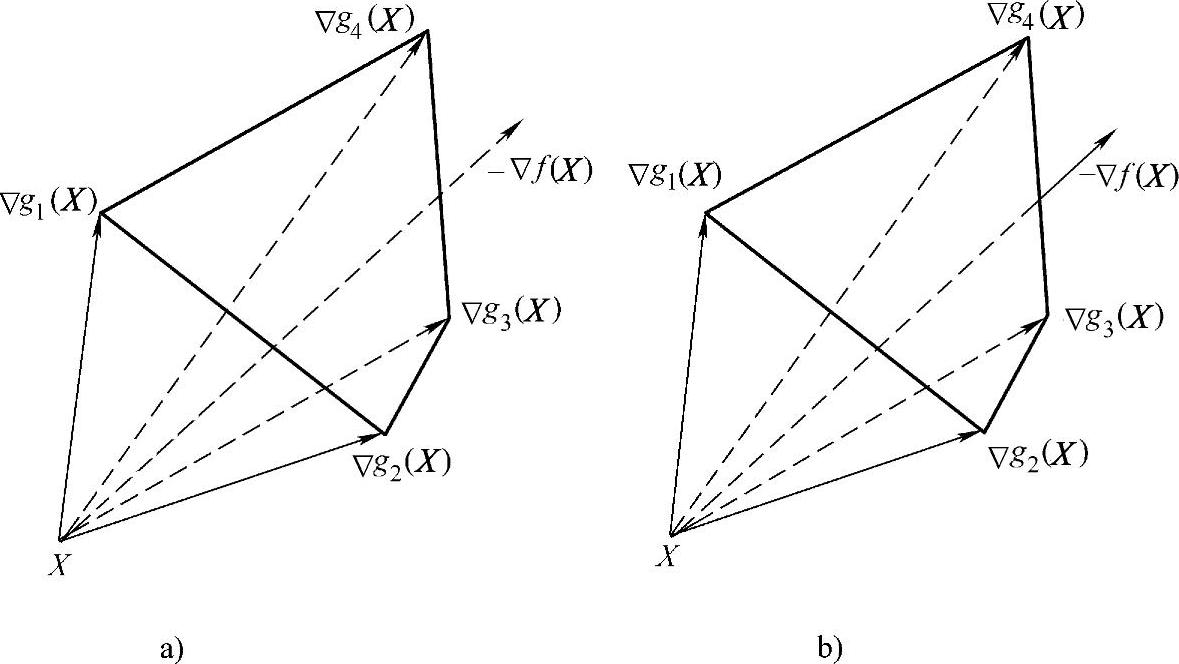
图2-9 K-T条件的几何解析