凸集与凸函数的分析介绍，

在讨论局部极小和全局极小的关系之前，先引入凸集和凸函数的概念。

1.凸集

设Ω为n维欧式空间中设计点X的一个集合，若其中任意两点x₁与x₂的连线都属于集合Ω，则称Ω是n维欧氏空间的一个凸集；否则为非凸集。凸集的几何解析如图2-4所示。

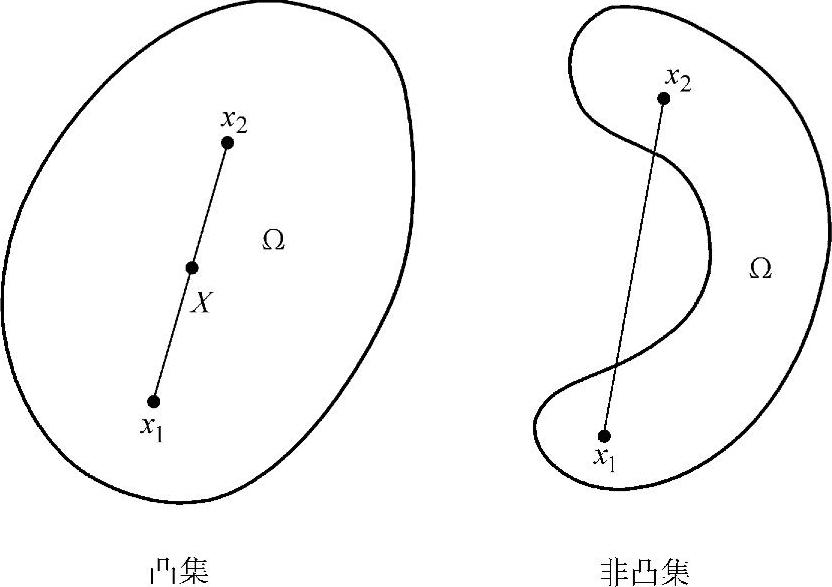
图2-4 凸集的几何解析

凸集的数学描述如下：在n维空间中，x₁和x₂连线上任意一点X可表示为

X=αx₁+（1-α）x₂ （2-23）

其中0＜α＜1。若x₁和x₂∈Ω，对应于α的一切值，均有X∈Ω，则Ω为凸集。

2.凸函数的定义(https://www.daowen.com)

设Ω为Eⁿ中的一个凸集，f（X）是定义在Ω上的一个函数，如果对于Ω内任意两点x₁和x₂，不等式

f（αx₁+（1-α）x₂）≤αf（x₁）+（1-α）f（x₂） （2-24）

对于一切0＜α＜1都成立，则称f（X）为Ω上的凸函数。

3.凸性条件（证明从略）

1）若函数f（X）在Eⁿ上可微，对于所有x₁∈Eⁿ，x₂∈Eⁿ，且x₁≠x₂，f（X）为凸函数的充要条件为

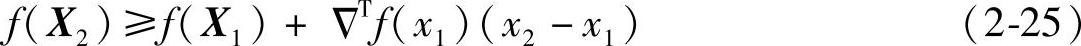
若上式以“＞”号成立，则f（X）为严格凸函数。

2）若f（X）为二阶可微，则f（X）在凸集上为凸函数的充要条件为：对于所有X∈Ω，海赛矩阵H（X）为半正定矩阵。H（X）对所有X∈Ω为正定矩阵，是f（X）在Ω上为严格凸函数的充分条件。