优化设计方法是使目标函数取得极值。我们知道，对于二元函数f（x₁，x₂），若在X₀（x₁₀，x₂₀）点处取得极值，其必要条件为

即 Δf（X₀）=0

为了判断X₀是否为极值点，还需要建立极值的充分条件。

若设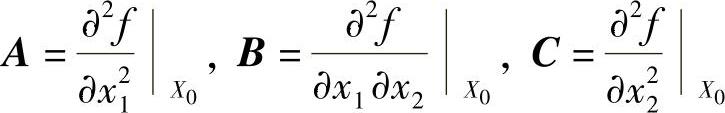

则式（2-19）可改写为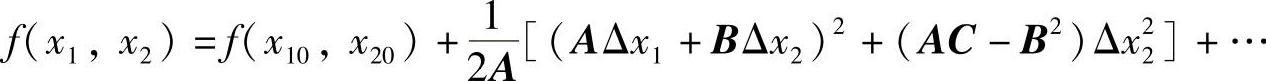

若f（x₁，x₂）在X₀点处取得极小值，则要求在X₀点附近的所有点X均须满足：

f（x₁，x₂）=f（x₁₀，x₂₀）＞0即要求

或 A＞0，AC-B²＞0

此条件反映了f（x₁，x₂）在X₀点处的海赛矩阵H（X₀）的各阶主子式均大于零。

即：二元函数在某点处取得极值的充分条件是要求在该点处的海赛矩阵为正定矩阵。(www.daowen.com)

对于多元函数f（x₁，x₂，…，x_n），若在X^*点处取得极值，则极值的必要条件为

极值的充分条件为海赛矩阵为正定矩阵，即要求H（X^*）的下列各阶主子式均大于零。

【例2-3】 求函数f（x₁，x₂）=x²₁+x²₂-4x₁-2x₂+5的极值。

解 首先，根据极值的必要条件求驻点。

得驻点为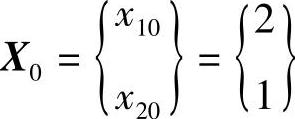

再根据极值的充分条件，判断此驻点是否为极值点。由于

而H（X₀）的一阶主子式和二阶主子式：

均大于零，故H（X₀）为正定矩阵，所以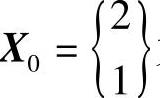为极小点，相应的极值f（X₀）=0。

一般说来，多元函数的极值条件在优化方法中仅具有理论意义。因为对于复杂的目标函数，海赛矩阵不易求得，其正定性就更难判定。