式（2-2）可改写成下面形式：

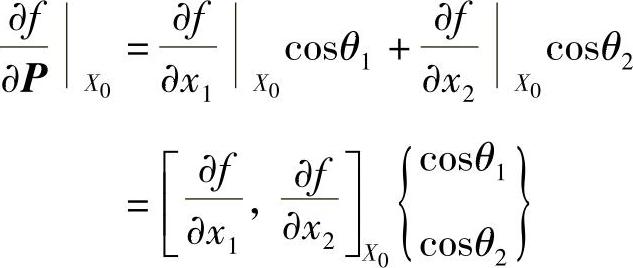
令

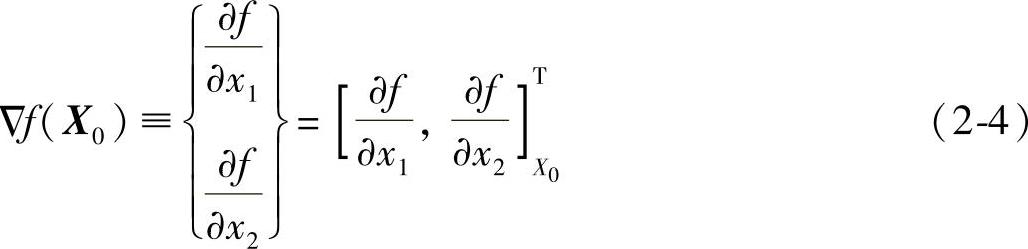
并称它为函数f（x₁，x₂）在X₀点处的梯度，其模为

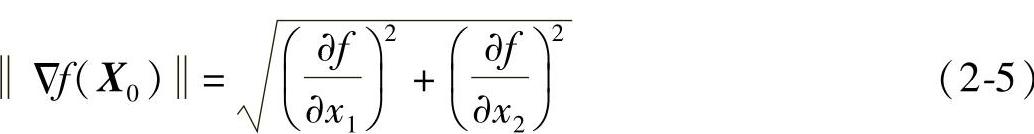
设 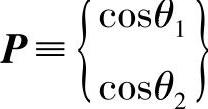为P方向的单位向量，则有

即函数f（x₁，x₂）在X₀点处沿P方向的方向导数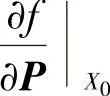，等于函数在该点处的梯度与P方向单位向量的内积。如果以θ表示两向量Δf与P的正方向之间的夹角，根据两向量的数积（或点积）的规定，则有

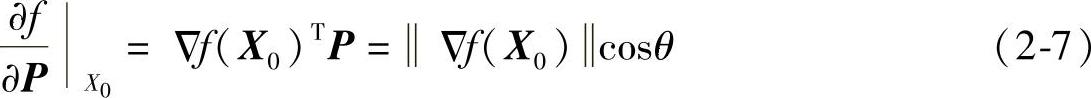
如图2-2所示，f（x₁，x₂）的等值线为

f（x₁，x₂）=C

C为任意常数，在X₀处等值线的切线方向P是函数变化率为零的方向，即有

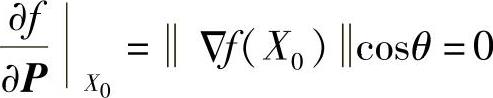
所以 cosθ=0

亦即梯度Δf（X₀）和切线方向P垂直，从而推得梯度方向为等值面的法线方向。当cosθ=1，亦即当梯度方向与P方向重合时，函数的变化率为最大[见式（2-7）]。可见梯度方向为函数变化率最大方向，也就是最速上升方向。负梯度方向为函数变化率取最小值方向，即最速下降方向。梯度的模就是函数的最大变化率。

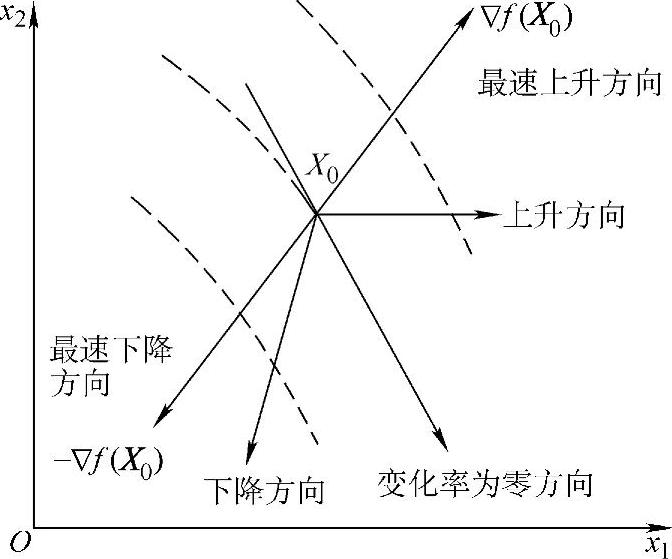
图2-2 梯度的几何描述

将二元函数推广到多元函数，对于函数f（x₁，x₂，…，x_n）在X₀（x₁₀，x₂₀，…，x_n0）处的梯度Δf（X₀），可定义为

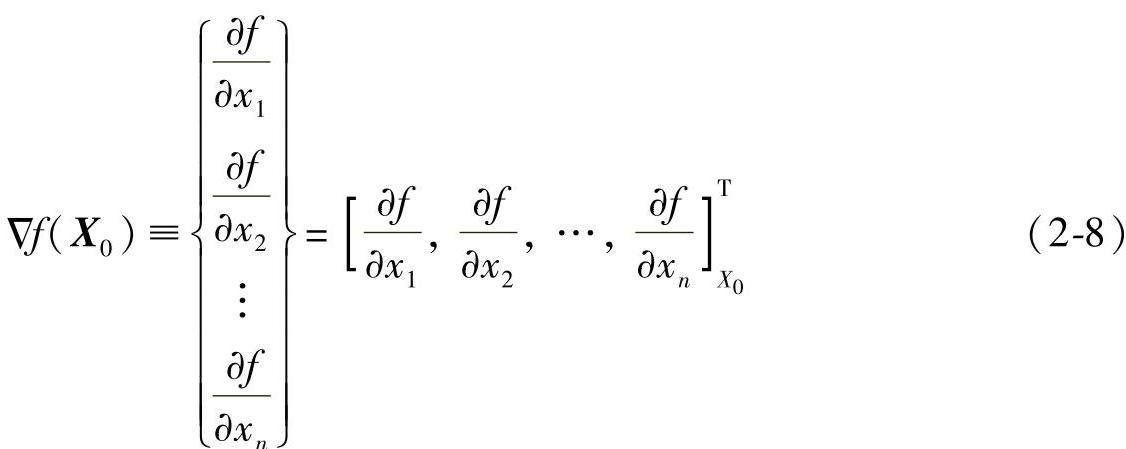(www.daowen.com)

沿P的方向导数可表示为

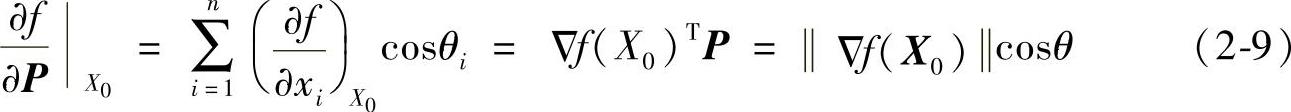
其中

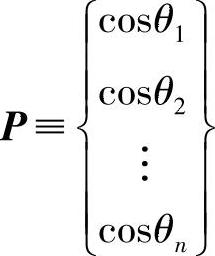
为P方向上的单位向量；

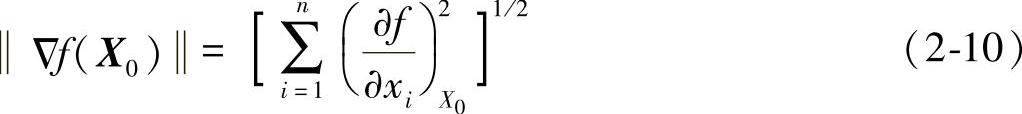
为梯度Δf（X₀）的模；

为梯度方向单位向量，它与等值面f（X）=C上过X₀的一切曲线垂直。

【例2-1】 求二元函数f（x₁，x₂）=x²₁+x²₂-4x₁-2x₂+5在X₀（0，0）^T处函数变化率最大的方向和数值。

解（1）先计算函数在X₀处的梯度

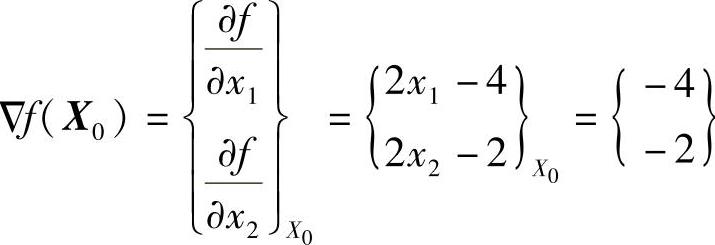
（2）函数变化率最大的数值是梯度的模

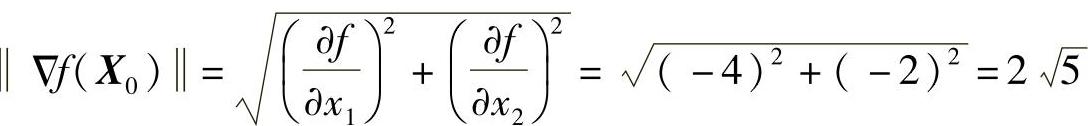
（3）函数变化率最大的方向是梯度方向

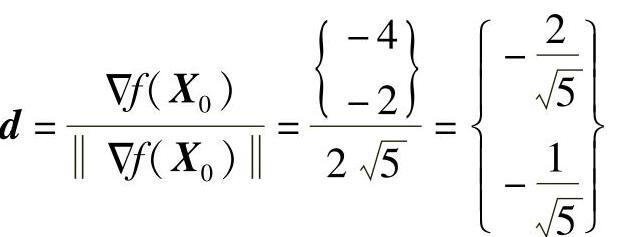
如图2-3所示，在坐标原点处函数变化率最大的方向d即为等值线的法线方向，也就是同心圆的半径方向。

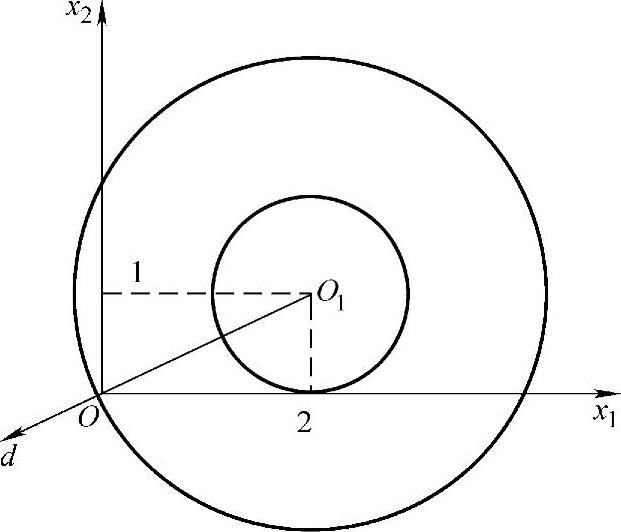
图2-3 例2-1解的几何表示