1.迭代过程

由前述知，无论是无约束优化问题还是约束优化问题，其实质均为求极值的数学问题。其寻优方法迥异于高等数学中的求极值方法，主要特点是：按照一定的逻辑结构进行反复的数值计算，寻求函数值不断下降的设计点，直到最后获得足够精度的近似解为止。此即为数值迭代法。

图1-7所示为一二维问题的迭代过程。从一选定的初始点X^（0）出发，沿某种优化方法所规定的方向，确定适当的步长，按下式产生新的设计点：

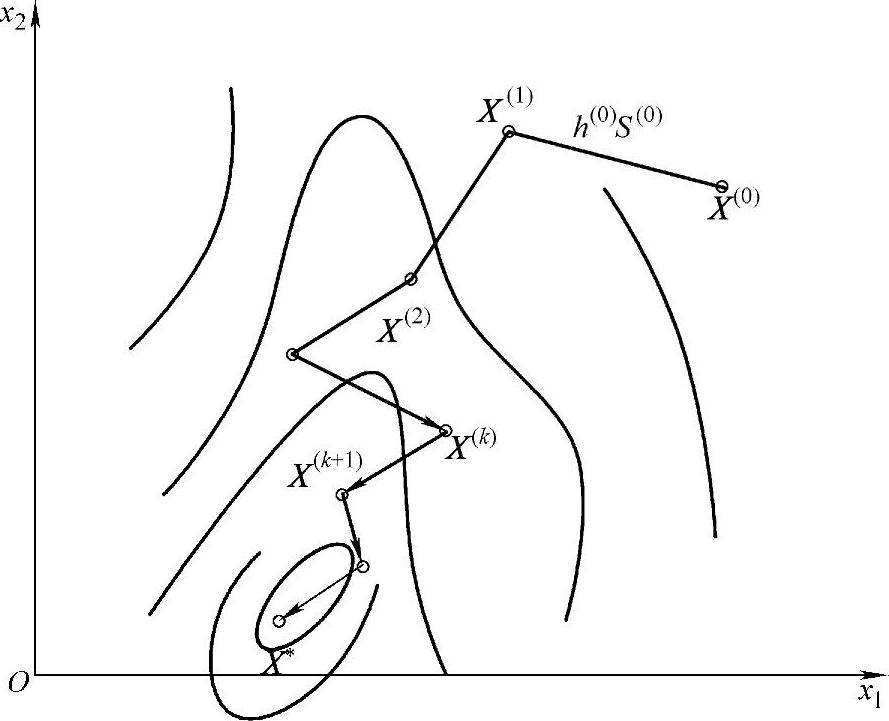
图1-7 二维问题的迭代过程

使满足

则X^（1）就是一个优于X^（0）的设计点。然后，以X^（1）为新起点按类似公式产生下一个新设计点：

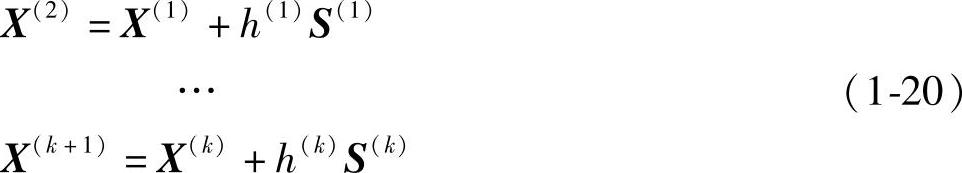
此即为优化计算所采用的基本迭代公式。应用上式，点列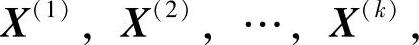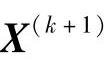都可通过同样的运算步骤作重复计算而获得，因而容易在计算机上实现。由于每一次迭代取得的新迭代点的目标函数值都有所下降，迭代点不断向最优点靠拢，因而最后必将达到十分逼近理论最优点的近似最优点X^*。

2.迭代计算的终止准则

上述迭代过程不可能无休止地进行下去，那么何时截断这种迭代呢？这就存在一个迭代终止的准则问题。

从理论上说，设计者当然希望最终迭代点到达理论极小点，或者使最终迭代点与理论极小点之间的差距足够小时才终止迭代。但是，这在实际中是难以实现的。因为对于一个待解决的机械最优化设计问题，其理论极小点在哪里往往并不清楚，所知道的仅仅是通过迭代计算获得的迭代点序列X⁽¹⁾，X⁽²⁾，…，X^(k)，X^(k+1)。因此，只能从点列所提供的信息及设计要求来判断是否应该终止迭代过程。(www.daowen.com)

对于无约束优化问题，常用的迭代终止准则有以下几种：

（1）点距准则 相邻两迭代点X^（k）与X^（k+1）之间的距离应小于或等于给定的允许误差ε（ε＞0），即

或写成：

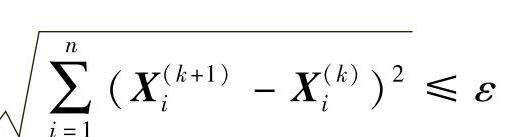
（2）函数下降量准则 当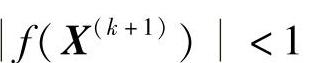时，用函数绝对下降量准则，即相邻两迭代点的函数值之差小于或等于给定的允许误差ε（ε＞0）：

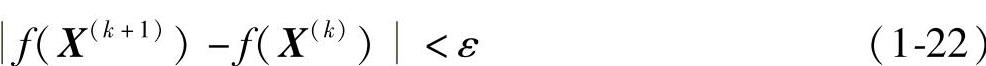
当|f（X^（k+1）|＜1时，可用函数相对下降量准则：

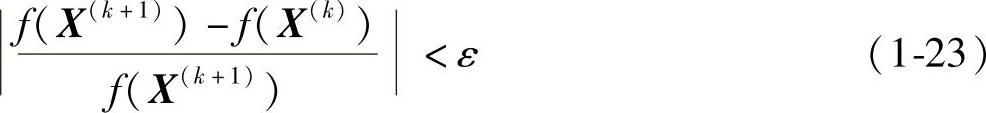
（3）梯度准则 目标函数在迭代点的梯度的模应小于或等于给定的允许误差，ε（ε＜0），即

必须指出的是，这一准则仅适用于目标函数于定义域上为凸函数。若是非凸函数，则有可能导致误把驻点作为最优点。关于函数的梯度、凸与非凸函数、驻点等概念将在第2章中详细论述。

对于约束优化问题，不同的优化方法有各自的终止准则（收敛条件），这将在第5章中逐一介绍。