用几何图形来解释非线性规划的最优化问题，可直观地表达出目标函数与设计变量和约束条件间的相互关系。

无约束优化问题就是在没有限制的条件下，对设计变量求目标函数的极小点。在设计空间中，目标函数是以等值面的形式反映出来，其极小点即为等值面的中心，如图1-5所示。

有约束优化问题是在可行域内对设计变量求目标函数的极小点，此极小点位于可行域内或在可行域边界上。如图1-6所示，可行域由线性约束方程（g₁（X）≥0）和非线性约束方程（g₂（X）≥0）围成，等值线为曲线，X^*为极小点，约束对极值点的位置影响很大。

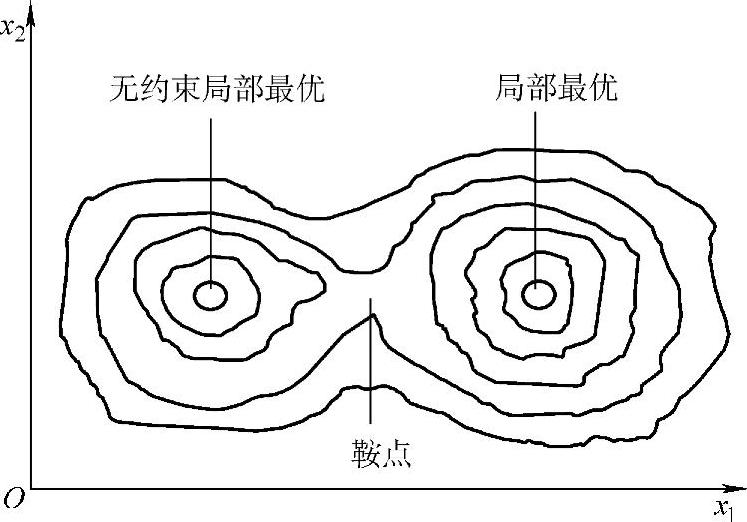
图1-5 无约束优化问题

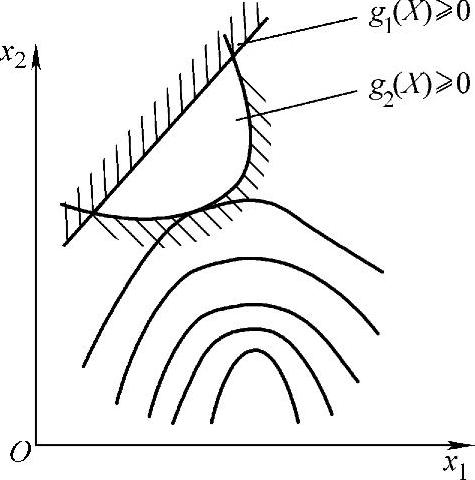
图1-6 有约束优化问题

综上所述，求n个设计变量在满足约束条件下目标函数极小化的问题，即为在n+1维空间的约束可行域内，寻找目标函数最小值X^*=[x₁^*，x₂^*，…，x_n^*]^T，并满足：(www.daowen.com)

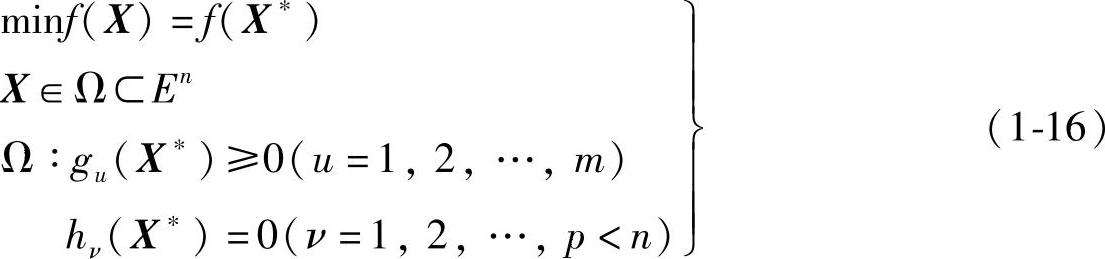
则称X^*为最优点（最优设计方案），f（X^*）为最优值。X^*和f（X^*）构成一个约束最优解。

如果一组设计变量仅使目标函数取最小，而并无约束条件，即满足：

则称为无约束最优解。显然，无约束最优解就是目标函数的极值及其极值点。

当目标函数不是单峰函数时，即有n个极值点x₁^*，x₂^*，…；则称x₁^*和f（x₁^*），x₂^*和f（x₂^*），…为局部最优解；而把其中最小者称为全域最优解（图1-5）。