设计空间是所有设计方案的集合。若设计方案满足所有对它提出的要求，就称为可行设计方案，反之则称为不可行设计方案。在机械设计中，有许多可行的方案，因而需要有一个衡量优劣的标准。在机械优化设计中，这个被用于评选设计方案优劣的函数，被称为目标函数或评价函效，记为

f（X）=f（x₁，x₂，…，x_n） （1-7）

机械最优化问题，就是要追求目标函数f（X）的极小化，常用下述形式表示：

式中 Eⁿ——n维欧氏空间。

在一个最优化设计问题中，可以只有一个目标函数，称为单目标函数，见式（1-7）。当存在两个以上目标函数时，称为多目标函数的最优化问题。在一般的机械最优化设计中，多目标函数的情况较多。目标函数越多，设计效果越好，但问题求解亦越复杂。对于多目标函数，可以独立地列出几个目标函数式：

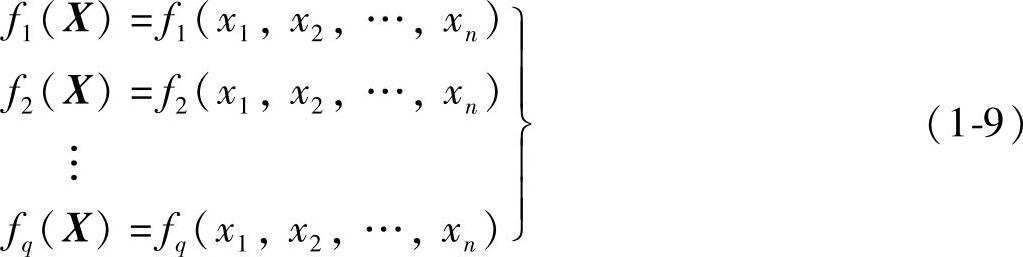
也可以把几个设计目标综合到一起，建立一个综合的目标函数表达式，即

(www.daowen.com)

式中 q——最优化设计所追求的目标数目。

为了方便求解多目标函数的优化设计问题，有时可引入加权因子的概念，用一个目标函数表示若干所需特性的加权和，从而转化为单目标问题求解。引入加权因子后，式（1-10）变为

加权因子w_j是个非负数，由设计者根据该项指标在最优化设计中所占的重要程度等情况而定。若该项指标的相对重要性一般，则取w=1。如何正确选择加权因子是一个比较复杂的问题，理论上尚未完善的解决，将在以后章节中具体说明。

目标函数与设计变量之间的关系，可用曲线或曲面表示。一个设计变量与一个目标函数的关系，是二维平面上的一条曲线（图1-4a）。当为两个设计变量时，其关系是三维空间的一个曲面（图1-4b）。若有n个设计变量时，则呈（n+1）维空间的超越曲面关系。

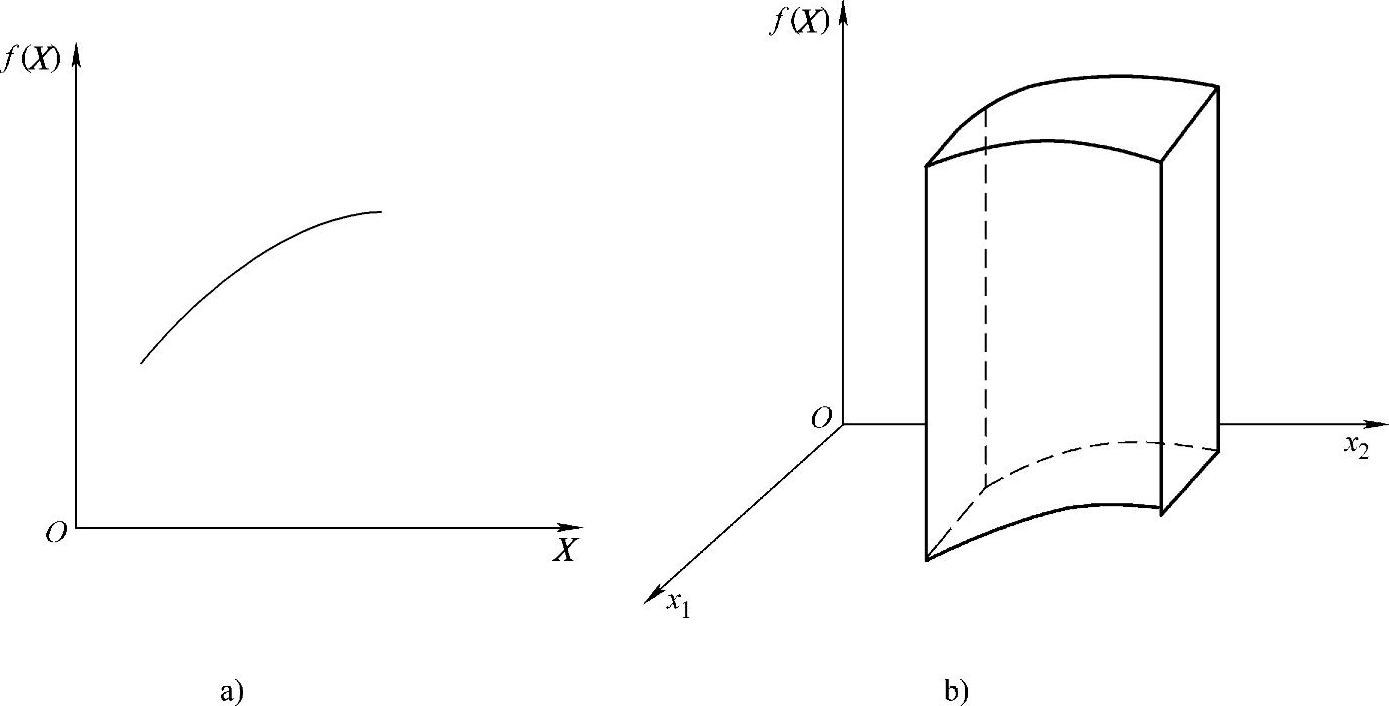
图1-4 目标函数与设计变量之间的关系