1.可疑观测值的取舍

处理力学性能试验结果时，特别是处理疲劳寿命试验结果时，常常会发现在一组数据中，某一观测值特别偏高或特别偏低，使人产生怀疑，称之为可疑观测值。对可疑观测值的取舍，不能采取随意的态度，而应科学严格地加以分析判别，然后决定取舍。

对可疑观测值的分析和判别，可从物理本质方面进行分析和从概率的观点进行数学处理。例如，对偏低的疲劳寿命，要检查试样的断口是否有夹杂、气孔，在疲劳源附近是否有表面划伤、锈蚀或加工刀痕等，试验过程中试验机是否产生了横振，鼓轮的跳动量是否超差等。经过分析，确系上述诸因素之一引起该试样寿命值偏低，才能作出取舍的决定。

从物理本质方面进行详细的分析而仍然不得要领时，可疑观测值的取舍可用数学判别的方法。这种判别方法的基础是在同一试验条件下，取得过大或过小的观测值，均属于小概率事件。根据实际推断原理，小概率事件在一次试验中几乎是不可能出现的，从而建立起取舍的判别准则。

（1）拉依达准则　在相同条件下测得一组观测值x₁，x₂，…，x_n，计算出均值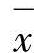和标准差σ为

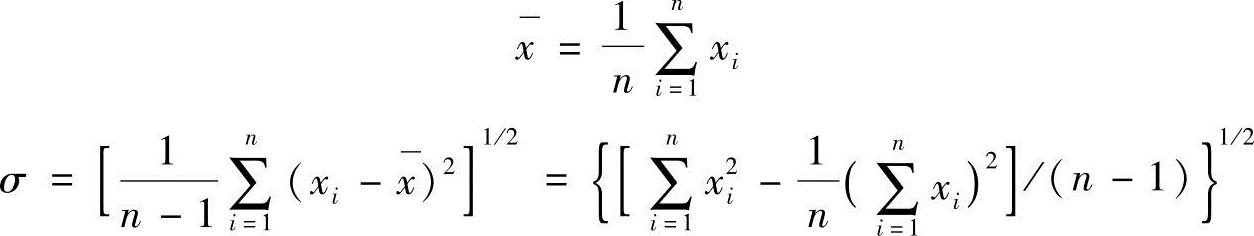
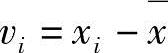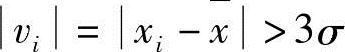如果x_i为可疑观测值，则计算偏差。如果，则舍去x_i，否则保留x_i。上式又称为3σ准则。例如已知某物体的温度经15次测量，其值如表1-16所示，求决定x₈=20.30℃的取舍。

表1-16　测量结果及处理

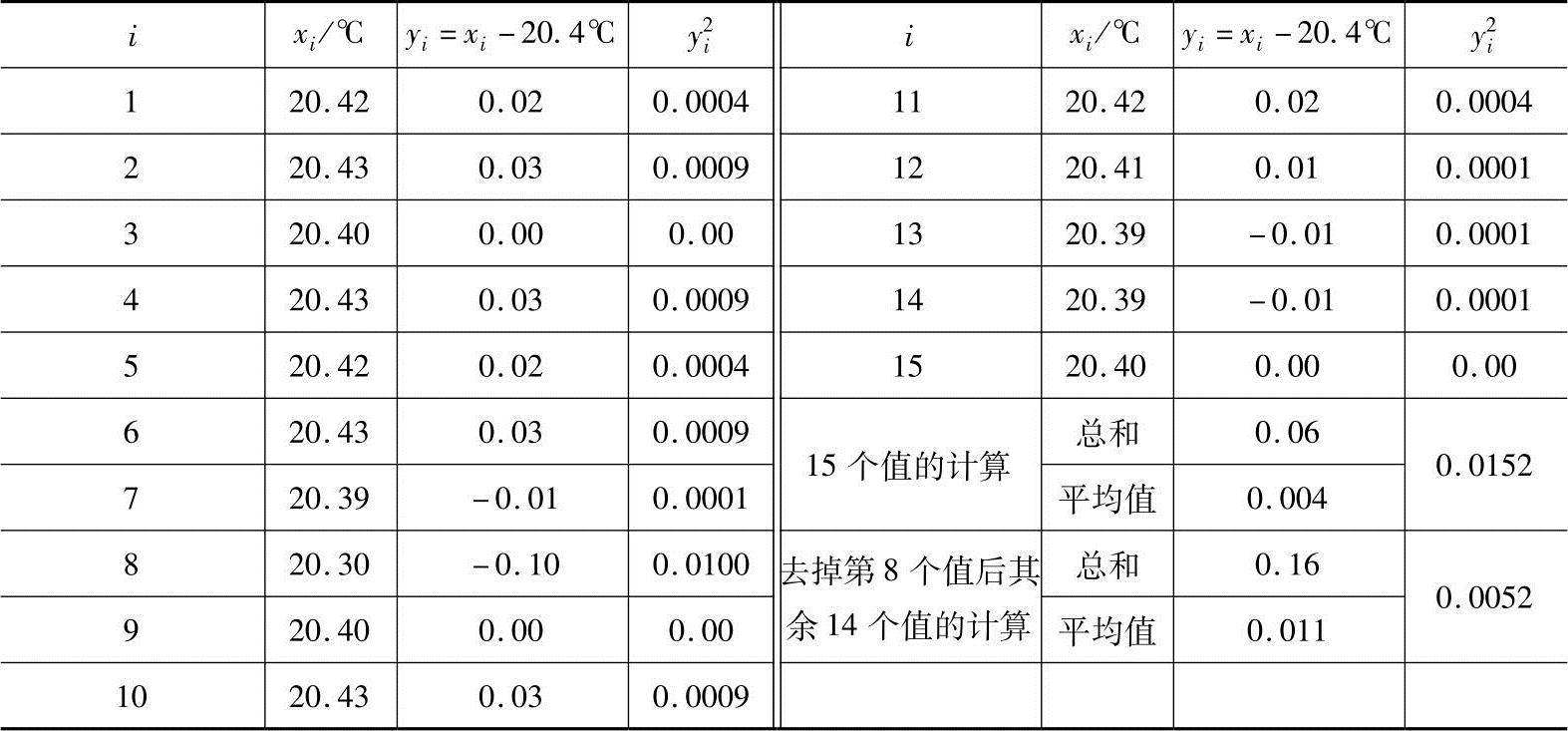
将15次测量的结果x_i及y_i=x_i-20.4℃和y²_i均列于表1-16。在计算x_i的标准差时，由于x_i的数值太大，可用y_i=x_i-b代替，这样由于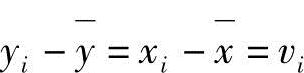，所以y_i的σ和x_i的σ是一样的，上例中，y_i的σ为

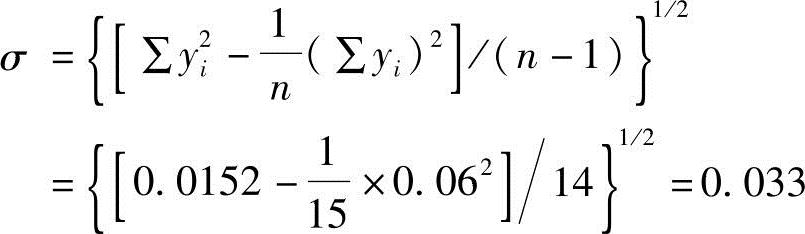
于是3σ=3×0.033=0.099，偏差绝对值v_i=x₈-20.404=-0.104>0.099，所以应该舍去x₈=20.30℃这个观测值。去掉x₈后，剩下的14个数据，作第二次计算，得σ=0.016，3σ=0.048，偏差x_i-20.411均小于3σ=0.048，均属有效。

（2）肖维奈准则(www.daowen.com)

该准则是根据正态分布原理得到的。在一组测量值x₁，x₂，…，x_n中，当可疑值x_i小于下限a或大于上限b时，则可舍去x_i。而a和b两个点是根据小概率1/2n来确定的。例如，设n=11，则1/2n=4.55%，a点以下和b点以上的正态曲线所包围的面积均为4.55%的一半即2.28%，如图1-28所示。查标准正态分布表，即可得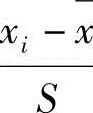

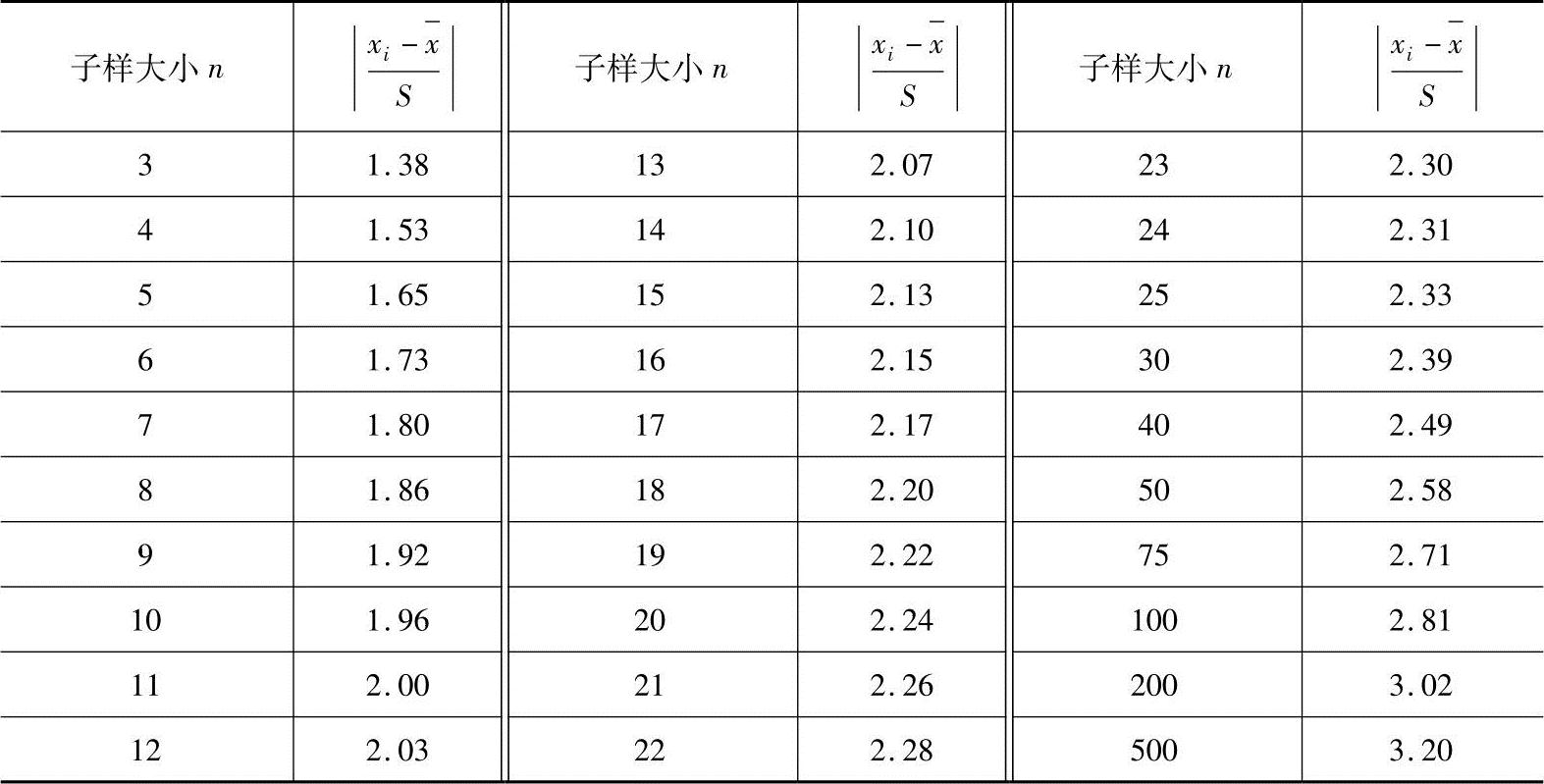
的限度，列于表1-17中。对于一组观测值中的某一可疑值x_i，只要其计算的绝对值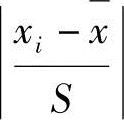超过相应的限值，则应舍去之，否则就应保留它。

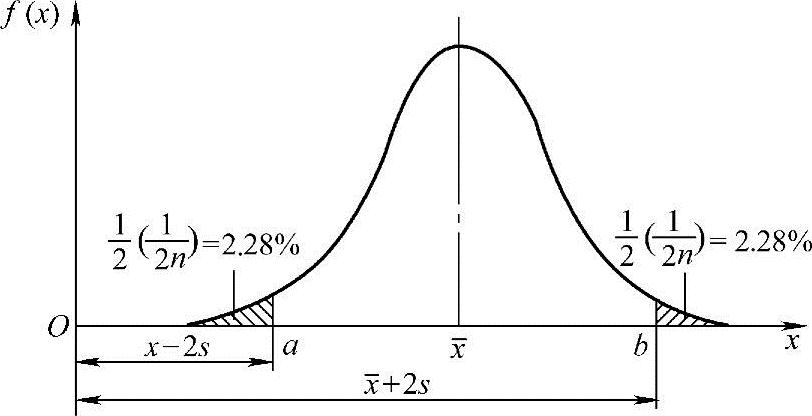
图1-28　肖维奈准则示意

上例中根据n=15，查表1-17得限值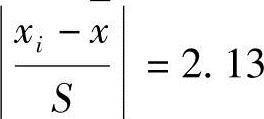。2.13×0.033=0.07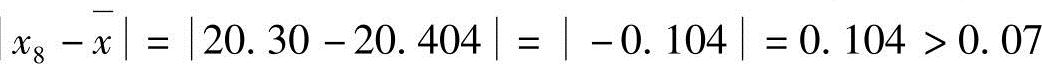，，所以舍去x₈，进一步计算：根据n=14，查表得限值为2.10，则2.10×0.016=0.034，舍去x₈后，其余x_i的偏差绝对值均未超过0.034，故均予以保留。

表1-17　肖维奈准则中的限值

2.对比试验结果的统计处理

力学性能试验往往会涉及到两种工艺、两种配方和两种设计方案的比较，这时就要作对比试验。例如，将欲对比的两组试样（一组经过喷丸处理，另一组未经喷丸处理），在同一加载条件下进行疲劳试验，根据疲劳寿命（或强度）的观测值，判别其疲劳性能是否相同，或其中的一组优于另一组。

由于疲劳试验结果的分散性，即使完全相同的两组试样，在同一台试验机及同一加载条件下进行试验，也会发现这两组试验数据的平均值和标准差存在着一定差异。当然，这种差异是由偶然误差所引起的，因此这种差异是不显著的。如果这两组试样是来源于两种材料，或一种材料的两种热处理，或两种不同的喷丸工艺等，这时两组试验结果的差异中，不仅包含了偶然误差，而且还包含了系统误差。这就要求对比试验结果的统计处理方法，能鉴别出这两组试验结果之间的差异是显著的（存在系统误差），还是不显著的（仅仅存在偶然误差）。

在对比试验中，有时关心的是两组试样平均值之间的差异，但有时也对两组试样的分散性（标准差）感兴趣，因此，对比试验结果的统计处理方法必须提供对母体平均值作假设检验和对母体标准差作假设检验的不同方法。