通过测量能直接得到结果的量，称为直接测定量，如人的高度和质量、拉伸试样的载荷和伸长量等。通过几个量的测量后要经过计算才能得到的量，称间接测定量，如物质的密度、材料的抗拉强度和断裂韧度等。

1.误差的分布规律

在不致引起误会的情况下常把偶然误差简称为误差。误差的特点如下：

1）绝对值相等的正误差和负误差，其出现的概率相同。

2）绝对值小的误差出现的概率大，而绝对值大的误差出现的概率小。

3）绝对值很大的误差出现的概率接近于零，即误差有一定的极限。

4）当测量次数n→∞时，误差的算术平均值趋近于零，这是由于正负误差互相抵消的结果。

2.误差的表示方法(www.daowen.com)

（1）范围误差　范围误差是指一组测量值中最大值与最小值之差，表示误差的变化范围。例如，对某钢材进行拉伸试验得到10个抗拉强度R_m（单位为N/mm²）的数据为745、750、751、759、763、766、770、781、784、785，则其范围误差为（785-745）N/mm²=40N/mm²。范围误差的优点是直观、简便，缺点是只取决于一组测量值的两个极端值，而与测量次数无关，与中间数据的大小无关，这显然与偶然误差和测量次数有关这一事实相违背。

（2）算术平均误差　是表示误差的较好方法，其定义为

式中　δ是算术平均误差；x_i是第i个观测值；x是n个观测值的算术平均值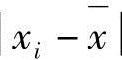；是偏差的绝对值。因为偏差有正有负，所以取绝对值加以平均。以上面10个R_m数据为例，其中x=765.4N/mm²计算得到δ=11.8N/mm²。算术平均误差的优点是比范围误差精细，考虑了每一个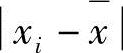；其缺点是无法鉴别两组测量值间的偏差大小。例如有两组测量值，尽管其δ可相等，但其偏差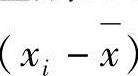可以很分散。

（3）标准误差　也称均方根误差，其计算式为

在观测次数n较小时，标准误差常表示为

标准误差σ是各观测值x_i的函数，且对x_i的大小比较敏感，所以是表示精密度的一个较好的指标，已广泛用于误差分析中。