1.误差的定义

一个物体的尺寸或质量、一种材料的抗拉强度或弹性模量等都存在一个客观真正的值，称为真值。在对各种物理量进行测量时，得到的结果称为实测值。误差就定义为实测值与真值之差，其式为

ε=x-x₀

式中　ε是误差，x和x₀分别是实测值和真值。

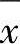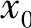1）在测量中，如果x₀代表某一物体的真实长度，x代表某一次的实测值，则ε=x-x₀就表示测量误差。由于真值x₀是未知的，在经过多次测量后，便可得到测量值的算术平均值，用x代替，便可得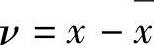，称ν为测量的偏差（或离差）。有时，可用对偏差的分析来代替对误差的分析。

2）在生产上，产品的某项技术参数往往给定一个标称值，这时将其作为真值x₀。误差ε=x-x₀就表示某一实测值与标称值之差。

3）在计算中，某物体的运动速度为（100±0.1）m/s，其中100m/s代表真值x₀，而±0.1m/s表示误差，称它为计算误差。

2.真值和平均值

由于测量仪器、测量方法、环境、人的观察能力等条件的限制，真值往往是无法测得的。但当测量的次数不断增加时，根据随机的正误差和负误差出现的概率相等并抵消的原理，在没有系统误差的条件下，平均值会趋近于真值。基于这种思想，用平均值（即子样的平均值）来估计和推断真值（在一定的量置信度下），并在条件许可的情况下，尽量增加测量次数。

（1）算术平均值　设一组观测值为x₁，x₂，…，x_n，n是观测次数，则算术平均值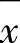定义为

假设观测值x_i服从正态分布，则可证明，在一组等精度的测量中算术平均值为最佳值。

（2）均方根平均值　这种方法来源于计算分子的平均动能，后推广用于误差的计算中，其定义为

（3）加权平均值　如对同一物理量用不同方法测定，或由不同的人员测定，则在计算平均值中常常对比较可靠的数据予以加权，然后再平均，称加权平均，其定义为

式中，x₁，x₂，…，x_n表示一组观测值；w₁，w₂，…，w_n对应于各观测值的加权数。

（4）中位值　将一组观测值按从小到大（或从大到小）的次序排列，则处在最中间位置的值就称为中位值。如果观测次数n为奇数，则排列在中间的那个数就是中位值。如果n为偶数，则中位值就是位于中间两个数的平均值。中位值的最大优点是求法简单，且与两端数据的变化无关，在数理统计中应用很广。

（5）几何平均值　一组n个观测值连乘，然后再开n次方得到的值称为几何平均值，其公式为(www.daowen.com)

上式两边取对数，则

上式说明，一组观测值取对数后的算术平均值，它的反对数就是这组观测值的几何平均值。

3.误差的分类

在测量中，无论所用的仪器多么精密，方法多么完善，试验者多么细心，所得结果往往也不尽相同。在生产中，尽管工艺和加工方法均一致，最后产品的尺寸、质量或其他技术参数也会存在差异。在计算中，计算工具的精度不同或计算方法不同也会带来不同的舍弃误差。

误差可按不同的方法分类。按误差的绝对值和相对值，误差可分为绝对误差和相对误差；按误差的性质及其产生原因，误差可分为系统误差、偶然误差和过失误差。

（1）系统误差　指在重复测量中，其值恒定不变或遵循一定规律变化的一类误差，又称为确定性误差或恒定误差。系统误差的来源主要有工具误差、装置误差、人身误差、外界误差和方法误差。

1）工具误差指由测量工具、仪器等产生的误差，又称为仪差。它是由于测量工具或仪器不完善而产生的，例如刻度不准、砝码未校正等。

2）装置误差指由于测量设备和仪器的电路、安装、布置和调整不恰当而造成的误差。

3）人身误差（个人误差或人差）指由于测量人员的感觉器官不完善而引起，例如某人在读数时视线总是偏向一边，从而造成读数误差，这种误差往往因人而异。

4）外界误差（环境误差）指由于周围环境如温度、气压、湿度和电磁场等的影响而产生的误差。

5）方法误差（理论误差）指由于测量方法本身所依据的理论、模型不完善所带来的误差。

系统误差的出现是有规律的，其产生的原因是可知的和能够找到的。对试验中所用的测量工具、仪器的精度进行鉴定，便可降低系统误差。对于不能消除的系统误差，要设法估计出其数值大小，以便进行修正。

（2）偶然误差（随机误差）　在消除了系统误差或降低系统误差至一定范围（例如拉力机载荷精度控制在±0.5%）后，对同一对象进行反复测量时，结果也会出现差异，这时产生的误差称为偶然误差。

偶然误差的特点是时大时小，时正时负，其产生原因是多方面的、不确知的，因而也是无法控制的。在同样条件下，对同一个物理量作重复测定，若测量次数足够多，则可发现偶然误差完全服从统计性规律。当测量次数无限增大时，偶然误差的算术平均值将趋近于零，因此多次测量结果的算术平均值将接近于真值。