高压是一种极端条件，指一切高于常压的压力条件，它作为热力学参数之一，其作用是温度或组分这种其他物理参量无法代替的。以材料科学为背景发展起来的高压物理学是研究物质在高压作用下的物理学行为的学科，是目前物理、化学及生物等学科领域创新的一个重要来源。目前高压物理的研究对象大部分是凝聚态物质，因此，在高压极端条件下研究凝聚态物质的性质我们称之为高压物理学。在自然界中，很多实体物质都处于高压状态，如地球的中心压力达到350万个大气压。高压科学将是人类认识自然的钥匙，它在当今科学研究领域中的作用不亚于与温度或成分有关的学科。

作为基本的物理学参量，压力可以使材料中的原子间距缩短，导致相邻的电子轨道重叠增加，从而改变材料的电子结构、晶体结构及原子分子间的相互作用关系，当达到高压平衡态时便产生全新的物质状态。这种在压力下产生的新物质状态具有不同于常压物质的新颖物理化学性质。研究表明，在100万大气压力下材料平均可以出现三个以上的相变，即压力效应可以给我们提供超出现有材料几倍的新物质，这极大地拓宽了我们寻找特殊用途新材料的途径。因此，研究稀土六硼化物在高压下的物理性质是很有必要的。Teredesai等人对LaB6进行高压拉曼测试及高压ADXRD（角散X射线衍射）测试，其中高压拉曼测试在单晶LaB6样品上进行，而高压（到20 GPa）ADXRD测试是在LaB6粉末上进行。其结果显示LaB6在10 GPa左右经历一个从立方相（空间群为）到正交相（空间群为Pban）的相变［22］。此正交相（a0=5.619Å，b0=5.732Å及c0=4.051Å）里La原子位于2a（0，0，0）位置，而B原子位于4l（0，0.5，0.2）和8m（0.15，0.36，0.335 9）位置。他们又用从头计算的FPLAPW方法，在局域密度近似下计算了压力下的LaB6电子结构。计算结果显示，没有压力时在布里渊区的Γ-M方向上有一条能带（d带）穿过费米能级。而当压力增加时此能带慢慢往上移，在13 GPa左右时正好移到费米能级上。这种费米面的拓扑变化可以称为电子拓扑相变（ETT）［23］。然而，Godwal等人对多晶LaB6样品进行的高分辨X射线衍射及拉曼光谱测试结果却表明，在0～25 GPa的压力范围内并没有发现结构或电子的相变［24］。他们室温下的拉曼测试及XRD测试都用了粉末样品，并且采用了高分辨测量提升了过去XRD测试的实验精度。他们的结果显示，一直到20 GPa的压力范围内T2g拉曼模频率在平稳增加，并且XRD图也表现出平滑的压力-体积关系。因此，需要更进一步地研究这些理论以及实验上的不同结果。针对此，我们采用第一性原理计算，从理论上研究了高压下LaB6的物理性质，详细讨论了高压下LaB6的电子结构、声子色散以及光学性质。

1.第一性原理计算细节

计算采用了基于密度泛函理论的CASTEP软件包，采用周期性边界条件，将价电子波函数用平面波基组展开。采用PBE框架下的广义梯度近似法处理交换关联势。选用La的5p 5d 6s态为外层电子，把其他电子视为原子核的一部分，用超软赝势描述价电子与离子实之间的相互作用势。平面波展开的截断能为Ecut=600 eV，自洽计算过程中体系总能量的收敛标准为1×10-6 eV/原子，作用在电子上的力不大于0.03 eV·Å-1。采用Monkhorst-Pack形式的特殊K点方法进行布里渊区积分，K网格的大小设置为24×24×24。在图6.3中给出的LaB6单胞结构上进行计算，并且能量计算都在倒易空间中进行，Gaussian展宽为0.5 eV。

采用密度泛函微扰理论（density functional perturbation theory，DFPT）的有限元位移法（又称超胞法）计算声子色散和声子态密度［25］。此方法中，构造超胞，根据体系的周期性把几个原子移动一下，计算原胞中所有原子所受的力，然后根据这个力构造力常数矩阵。

2.相结构及电子特性

在0 GPa下结构优化得到的LaB6晶格常数a以及内部参数z分别为4.160 6Å和0.200 1，与实验值的偏差小于0.2％。随着压力的增加，LaB6的晶格常数线性减小。在图6.15中我们画出了计算得到的LaB6单胞相对体积变化随着压力的变化关系图，并与Torsten等人从实验上测得的值进行了比较［26］。从图6.15中可以看出我们的计算结果与实验结果很好地符合。

图6.15　-ΔV/V与压力的变化关系计算结果与实验值的对比［26］

众所周知，材料最稳定的结构拥有最低的Gibbs自由能（G=U＋PVTS），因此在零温时具有最低的焓（H=U＋PV）。为了弄清LaB6在压力下的相变情况，我们对它和可能存在的Pban结构的焓进行了计算，结果在图6.16中给出。结果显示和Pban结构的焓差非常微小，很难区分，并没有出现两种结构的焓随压力的变化曲线相交于某一点的情况。此外我们又计算了其相对焓的变化，也没有得到有意义的结果。Xu等人把Pban结构看作另一个稀土六硼化物YB6的假想高压结构，并对YB6进行了计算，在计算精度之内同样没有分辨出和Pban结构的焓差［27］。因此，从焓差计算上不能够确定Teredesai等人报道的LaB6在10 GPa左右出现的相变。

图6.16　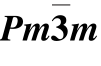和Pban结构的焓随压力的变化关系

图6.17为LaB6在0 GPa下的能带结构图，费米能级取为能量为零处。从图中可以清楚地看到，布里渊区的X-R方向及M-Γ方向上都有一条能带穿过费米能级。为了与前人的计算结果比较，我们在图6.18中给出了LaB6在0～45 GPa压力下M-Γ方向上的能带图（d能带）。随着压力的不断增大，此d能带的位置慢慢往上移，当压力增大到45 GPa的时候能带底已经移到了费米能级的上面，也就是发生了所谓的电子拓扑相变或者Lifshitz相变［28］。我们计算得到的ETT点在45 GPa左右处，而Teredesai等人采用FPLAPW方法计算得到的相变点在13 GPa左右处［22］，然而之后的高分辨X射线衍射以及拉曼光谱测试结果并没有在13 GPa附近发现任何相变［24］。Xu等人计算的YB6的ETT点出现在40 GPa处［27］。由于此d能带在很大的压力范围内随着压力的移动非常微小，因此采用不同方法计算得到的结论也会有很大的区别，我们的计算结果与高分辨X射线衍射及拉曼光谱测试结果相吻合。

图6.17　LaB6在0 GPa下的能带结构图

图6.18　LaB6在0～45 GPa压力下M-Γ方向上的能带图

Lifshitz指出如果一个外部参数，如压力的变化导致费米面拓扑结构的变化，它很可能会影响态密度的单调变化［28］。图6.19中我们画出了不同压力下LaB6的总态密度（TDOS）以及费米能级处的分态密度（PDOS），费米能级取为能量为零处。从图6.19中可以看到，TDOS在费米能级处比较平坦，并且随着压力的增大而减小。费米面附近的电子态展现出很强的杂化特性，除了La 5d态以外所有La和B的PDOS随着压力的增大而减小。La 5d态在35 GPa左右达到最小值，压力继续增大时又开始增大。然而La 5d态对费米面附近总态密度的贡献非常小。Medicherla等人的高分辨光电子能谱研究结果显示，在低温下（T＜100 K）LaB6有赝能隙［29］，可能与LaB6的低能声子模有关。

为了弄清LaB6在压力下的键合行为，我们对其进行了Mulliken电荷布局分析。图6.20为计算得到的LaB6在不同压力下的（110）面差分电荷密度图。LaB6有两种B-B键，如图1.1中所示，一个是连接两个相邻B6八面体的BB1键，另一个是B6八面体内连接两个相邻B原子的BB2键。从图6.20中可以看出BB1键上的电荷密度远大于BB2键上的电荷密度，并且B原子之间的电荷密度也大于La原子与B原子间的电荷密度，表明B原子和B原子间为共价键性质而La原子和B原子之间为离子键性质。随着压力的增大，B原子和B原子间的电荷密度也在增加。在图6.21中给出计算得到的详细的Mulliken有效电荷（MECs）。从图6.21中可以看出，La的正电荷随着压力增大而增加，而B的负电荷随着压力的增加而减小，表明压力会导致电荷从La原子到B原子的转移。B原子的MECs随着压力展现出阶梯变化的现象，可能是因为B原子的MECs远小于La原子的MECs，而且随压力的变化也很小。在0 GPa时，从La原子到B原子的电荷转移量为2.57 e，表明LaB6里La的有效离子价态为＋0.43。而随着压力的增加，在40 GPa的时候La的有效离子价态减小到＋0.23。上面的现象表明，随着压力的增加，LaB6的共价键特性在变弱而离子键特性在变强。

图6.19　不同压力下LaB6的总态密度以及费米能级处的分态密度

图6.20　计算得到的LaB6在不同压力下的（110）面差分电荷密度图

3.声子(www.daowen.com)

图6.21　B原子和La原子的MECs随压力的变化关系

图6.22　计算得到的在0 GPa下LaB6沿布里渊区高对称点的声子谱以及对应的声子态密度

（a）0 GPa下LaB6声子谱；
（b）对应声态密度（红点为Smith等人的实验结果）［30］

声子可以用来描述晶格的振动，是固体理论中非常重要的一部分。从声子谱的计算中可以研究材料的热力学性质，从声子软化与否可以判断材料结构的稳定性。图6.22为计算得到的在0 GPa下LaB6沿布里渊区高对称点的声子谱以及对应的声子态密度，同时给出了Smith等人从实验上测得的LaB6声子谱作为对比［30］。我们的计算结果和Gürel与Eryigit的计算结果一致［31］，与实验结果除了在R点处声子频率400 cm-1附近有差别之外很好地吻合。根据文献［27］、文献［31］，实验与理论在布里渊区R点处的差别可能来自两个原因：一个是样品大小和高能下的低中子通量导致在实验上布里渊区R点处的不准确测量结果。另一个是在DFPT理论框架里没有考虑在R点处的有些过程。从图6.22（a）中可以看出，对LaB6的声学声子模有贡献的La离子的振动位于低频范围内，且渐离布里渊区高对称点的声学模变得非常平坦，导致了在图6.22（b）中的低频声子态密度形成了非常尖锐的峰。LaB6在0 GPa下展现的声子色散特性与YB6和SmB6的非常相似［27，32］。

LaB6的原胞含有7个原子，按照群论，空间群的Wyckoff位置1a和6f的Γ点上产生的振动有

式中，R为拉曼活性模；IR为红外活性模；T1g和T2u在光学上是非活性的。图6.23中给出了在声子谱的Γ点上频率随压力的变化关系。在0 GPa时，计算得到的A1g、Eg和T2g模的频率分别在1 266 cm-1、1 125 cm-1及710 cm-1，与从拉曼散射实验得到的1 258 cm-1、1 120 cm-1及682 cm-1吻合［33］，计算误差小于5％。随着压力的增加，所有的声学模和光学模都往高频处移动。从图6.23中可以看出Γ点上的这些模的频率都有随着压力的增加而增加的趋势，T2g模随着压力的增加而线性增加的趋势与拉曼测试结果一致［24］，计算结果里没有发现声子软化现象。通常，声子软化到零频处的行为表明材料在结构上的不稳定。因此，在压力下对声子谱的计算也没有表现出LaB6从到Pban相的转变。这一点与YB6不同。对YB6，其R25和M2声学模在54.5 GPa时已软化到零频处［27］，而YB6的ETT相变出现在40 GPa处。因此我们可以推断，声子软化与ETT相变并不直接相关。

图6.23　在声子谱的Γ点上频率随压力的变化关系

4.光学性质

在图6.24中我们给出了在不同压力下计算所得的LaB6介电函数的实部与虚部。从图6.24中可以看出，LaB6的光学性质在45 GPa时发生了明显的改变。LaB6的介电函数在0～35 GPa的范围内服从Drude模型，Drude模型可以表示为［34］

式中，ωp=（Ne2/mε0）1/2为等离子频率；τ为阻尼项。基于自由电子气近似的Drude模型通常适用于金属材料，它忽略了所有电子与电子之间或电子与离子之间的长程相互作用，自由电子本身所处的环境当中唯一可能的相互作用是通过瞬时碰撞而来的。当压力上升到45 GPa时，LaB6的介电函数转变为服从Lorentz模型，Lorentz模型可以表示为［34］

式中，ω0为振荡频率。Lorentz色散理论基于阻尼谐振子近似。

图6.24　在不同压力下计算所得的LaB6介电函数的实部与虚部

LaB6的光学性质在45 GPa时显示的明显变化的原因是布里渊区M-Γ方向上的d能带的移动。在图6.18中，45 GPa时M-Γ方向上d能带的最小值已经移到了费米面之上，因此导致了光学性质上的明显变化。LaB6介电函数的虚部在0.12 eV处出现的峰对应图6.18中的两个能带之间电子的跃迁。在0 GPa时M-Γ方向上的d能带穿过费米面，因此有电子能够从图6.18中的下能带跃迁到上能带。而在45 GPa，由于d能带已经移到费米面之上，不再有电子从d能带跃迁到上面的能带。因此，在45 GPa时介电函数的虚部的低能量处（0.12 eV左右）没有出现峰。我们对能带结构的计算结果显示，布里渊区X-R方向上的一条导带在45 GPa时仍然穿过费米面，表明此时LaB6还是显示金属特性。因此可以推断，X-R方向上的那条能带对LaB6的光吸收没有贡献。随着压力的增加，介电函数虚部里位于4.3 eV和6.1 eV处的两个主峰往高能量处移动，这是因为相对应的能带距离随着压力的增加而变宽了。

在图6.25中给出不同压力下LaB6的能量损失谱。在0～35 GPa的压力范围内，1.5 eV左右能量处的第一个等离子共振峰随着压力的增大往高能量处移动，而压力增加到45 GPa时，此峰消失，这与介电函数的变化一致。由于第一个等离子共振峰的位置对应LaB6在可见光区吸收谷的位置，因此我们的计算结果表明可以通过压力来连续调控LaB6在可见光区吸收谷的位置。从图6.25中还可以看到，在0～35 GPa的压力范围内，第一个等离子共振峰的强度也随着压力的增大而增大，表明在一定压力范围内，LaB6将会展现出更好的隔热性能。而其随着压力发生这种光学性质上的变化跟其费米面附近电子的状态有关系。在图6.26中画出了LaB6在不同压力下的费米能绝对值。从图6.26中可以看出，LaB6的费米能绝对值随着压力的增大而增大，说明费米面附近的电子在压力下拥有了更大的动能，导致其等离子共振峰随压力的变化而变化。

图6.25　不同压力下LaB6的能量损失谱

图6.26　LaB6在不同压力下的费米能绝对值