由式（5-7）可知，当x≥x_e时，则有

x_r＝f_r/k_e＋x_e （5-29）

工作中参考位置x_r被指定为一个恒量，即有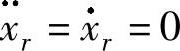。若f_r为恒量，则有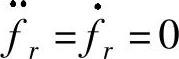，将式（5-29）代入式（5-3c），则所定义的目标阻抗模型为

稳态力误差为［152］

式中 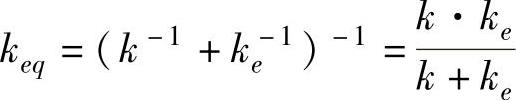——目标阻抗和环境的等效刚度。稳态接触力为

从式（5-31）可知，稳态力f_ss与参考力f_r及参考轨迹位置x_r的函数关系，在参考位置满足式（5-29）时，稳态力误差e_ss＝0。当环境位置x_e和环境刚度k_e精确可知时，实现无误差的参考力轨迹跟踪的条件是按x_r＝f_r/k_e＋x_e来选择参考轨迹位置x_r。然而，环境刚度k_e和环境位置x_e的精确值很难在实际操作中获得。通常取估计值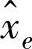和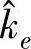，设Δx_e、Δk_e为实际环境位置和环境刚度与假设的环境位置和环境刚度间的差，则有(www.daowen.com)

式中 x_e、k_e——实际的环境位置和环境刚度；

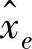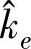、——环境位置和环境刚度的估计值。

使用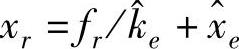定义的参考位置时的稳态力误差为

采用直接对环境参数进行估计的方法，可解决环境刚度、环境位置不确定引起的力误差。由于环境刚度k_e通常很大，由式（5-34）可知，即使取很小的环境位置偏差Δx_e，力控制误差值也会很大。若使阻抗控制能完成精确的力控制任务，实时对环境参数在线估计是最直接的办法。