根据Hogan^［74］提出的阻抗控制概念可知，对力和位置偏差的期望关系进行调节是阻抗控制的关键，建立的期望关系称为目标阻抗，如式（5-1）所示。

F-F_r＝Z（X-X_r） （5-1）

式中，F、F_r、X、X_r分别为机械手与环境的接触力、期望力、位置和期望位置。

在质量—弹簧—阻尼系统表示的阻抗如图5-1所示。机械手末端与环境相互接触产生作用力，发生形变。对于机器人工具末端位置偏离期望轨迹的差和末端与外界间的相互作用力，建立的目标阻抗可用如下二阶微分方程描述，式（5-2）给出了常用的目标阻抗三种数学表达形式^［159］。

式中 X_r（t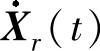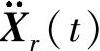）、、——机器人终端的参考位置、速度和加速度向量；

X、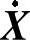、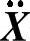——x、y、z方向3×1的机器人终端位置、速度和加速度向量；

M_d、B_d、K_d——3×3的目标惯量矩阵、目标阻尼矩阵和目标刚度矩阵；

F——x、y、z方向3×1的机器人工具端与环境接触时，环境作用给机器人工具端的力向量。(www.daowen.com)

为达到力跟踪的目的，在上面的研究基础上，采用实际接触力与期望接触力之差e_f＝F_r-F代替式（5-2）中的环境作用力F，作为目标阻抗模型的驱动信号，得到新目标阻抗模型为

图5-1 式（5-2）物理模型

令E＝X-X_r，采用式（5-3c）表达的目标阻抗模型为

在笛卡儿坐标系各个坐标轴方向是解耦控制时，目标惯量矩阵M_d、目标阻尼矩阵B_d、目标刚度矩阵K_d和环境刚度矩阵K_e一般都可取为对角正定矩阵，因此可以进行简化，只考虑机器人操作空间某一维的情况，分析机器人笛卡儿坐标系任意一坐标轴方向的阻抗控制，可用f_r、f、m、b、k代替F_r、F、M_d、B_d、K_d、并令e＝x-x_r则式（5-4）变为

在自由空间和约束空间中分别考察机器人的两个运动。因自由空间中，研磨工具末端接触力f＝0，则有

式中，若能得到精确的环境位置，如果设参考力f_r为0，工具端的驱动力决定了期望力，机器人将与环境保持接触，使机器人对环境施加力。