基于系统在操作点线性化并设计相应的线性控制器是一种常用的求解非线性控制的方法，控制器可以保证系统是局部稳定的，并决定了整个系统的稳定性。如在设计中引入速度滤波函数，选用合适的李亚普诺夫函数可以证明线性控制器是全局稳定的^［110］。

机器人的比例加微分（PD）控制规则就是基于这样的设计思想，最简单的PD控制规则具有如下形式：

式中，K_v和K_p为正定矩阵，e＝q-q_d。参考文献［150］中分析了基于PD的3种常用机器人轨迹跟踪算法的控制性能，鉴于上述的控制规则不能获得准确无误差的轨迹跟踪，可通过在控制结构中加入前馈项的方法，消除静态误差并提高轨迹跟踪精度。

本文采用的PD＋前馈滑模变结构控制框图如图4-1所示^［158］。

对应图4-1的总控制律为

式中的前馈项为

图4-1 PD＋前馈滑模变结构控制框图

从而控制律为

对于本文的5自由度机器人，动力学方程式（4-6）可表示为

式中，表示摩擦力，表示外界干扰，其他具体参数意义描述见前述。定义e＝q-q_d，并将控制律式（4-15）代入式（4-18）与式（4-19）中，可得到闭环的动力学方程

式（4-20）和式（4-21）中Δ为各类不确定性的集合，如果摩擦力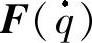及外界干扰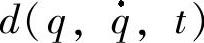的影响被忽略，且系统的参数误差不存在，只需要将前馈项取为

此时，不确定项Δ＝0，但是不存在这样的理想情况，需要设计τ_s以补偿不确定项Δ。

采用前馈控制律式（4-17），则不确定项Δ为

本文不加证明，基于如下假设，应用控制理论进行研究。

1）期望轨迹q_d满足sup‖q_d‖≤c₀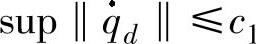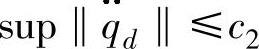，，；其中c₀、c₁、c2＞0

2）惯性矩阵有：‖M（q）‖≤k_m，‖M₀（q）‖≤k_m0，其中k_m、k_m0为正常数。

3)，，其中k_c、k_c0为正常数。

4）对重力项有：‖G（q）‖≤k_g，‖G₀（q_d）‖≤k_g0，其中k_g、k_g0为正常数。

5）对摩擦力项有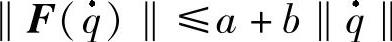：，其中a、b为正常数。(www.daowen.com)

6）对干扰项有：，其中d₀、d₁、d₂为正常数。

滑模函数定义为

其中，Λ是正定对角矩阵，Λ＝λI，λ＞0。

结合补偿控制器设计思想，利用约束函数η，设计一个具有时变边界层的滑模补偿控制律如下：

式中滑动变量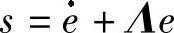，Λ＞0，ε（t）＞0是待定的边界层厚度函数。可适当地选取ε（t），对控制精度加以保证，从而使控制力矩光滑。

定理4-1 对机器人动力学方程式（4-18）和式（4-19），采用式（4-17）的控制结构，则滑模补偿控制律式（4-25）使得闭环的动力学方程式（4-21）达到最终一致有界稳定^［158］。

证明：取Lyapunov函数为

式中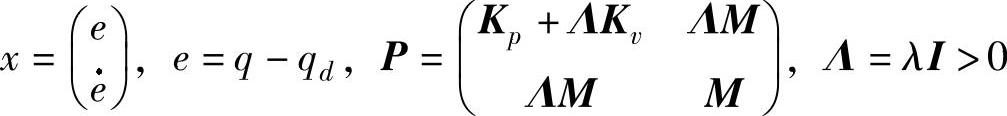，0。

只要适当选择较小的常数λ，根据矩阵理论可知，就可以保证矩阵P正定。

对式（4-26）求导，并代入闭环的动力学方程式（4-21），可得

-x^TQx＋s^TΔ＋s^Tτ_S （4-27）

式中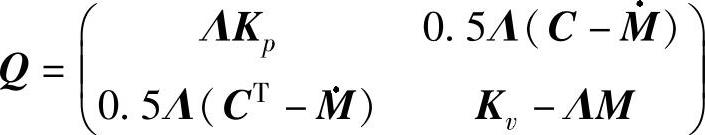，。要使Q＞0必须有K_v-ΛM＞0

只要选择足够大的K_p和K_v，以及充分小的Λ，上述不等式就可以保证成立，从而有Q＞0。再将滑模补偿控制律式（4-25）代入式（4-27）得

当‖s‖＜ε（t）时，式（4-28）第二项有

欲使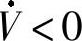，须有

根据关系式

λ_min（Q）‖x‖²≤x^TQx≤λ_max（Q）‖x‖² （4-30）式中，λ_min表示最小特征值，λ_max表示最大特征值。当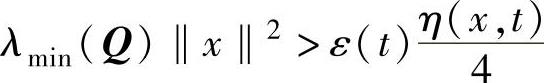时，。上式等价于

取B（r）为中心在x＝0，半径为r（t）的闭球，在闭球B（r）外面，有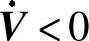，所以只要x（t）∉B（r），有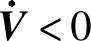，在有限的时间T内，x（t）达到闭球的边界。取t′＝t₀＋T（t₀为任意初始时刻）为系统状态达到闭球边界的时间，则当t≥t′时，x（t）∈B（r）。根据最终一致有界的定义，可得采用滑模补偿控制律式（4-25）时，闭环系统为最终一致有界。