在实际机器人系统中，由于存在着建立被控对象数学模型局限性问题以及实际过程自身参数摄动现象，因此，机器人系统中不可避免地存在着各种形式的不确定性^［110］。

1）参数不确定性：一般不改变系统的结构及阶次，如负载、连杆质量及连杆几何参数。

2）非参数不确定性：低频未建模动力学特性，包括各关节的摩擦、关节柔性等。建模时忽略的高频特性，包括驱动器动力学特性、结构共振模式等；作业环境干扰、驱动器饱和问题，测量误差、舍入误差及采样延迟等。

因此，很难得到式（3-3）表示的精确动力学模型。控制系统无法通过常规的线性控制方法得到理想的效果，对机器人系统的分析和研究，必须按照非线性系统理论处理。为提高机器人的工作性能与实现系统的鲁棒性，上述不确定性的影响因素，在设计实际机器人动态控制系统时，必须加以考虑。结合上一章的动力学模型，在充分考虑这些不确定性因素和机器人的受限运动情况下，对于本文的机器人系统可得到如下完整动力学模型

式（4-6）中，考虑了机器人的不确定因素后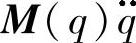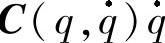，、、G（q）在物理意义上与式（3-3）是一样的，但是此时的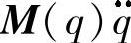、、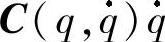G（q）是时变量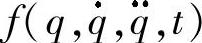；表示外界扰动量（包含非参数不确定性、模型不确定性），τ为作用在关节上的5×1维力/转矩矢量。

本文中将式（3-3）称为机器人的标称系统模型，式（4-6）称为机器人的实际系统模型。

关节速度和笛卡儿空间速度的关系可以表示为

根据表示操作器末端点实际位移和关节实际位移关系的雅克比矩阵J_q（q），笛卡儿加速度项可写为

关节空间机器人的运动方程在笛卡儿空间坐标系中表示为(www.daowen.com)

在雅克比矩阵J_q（q）的非奇异的位置，根据关节空间与操作空间的速度、加速度关系，由式（4-6）、式（4-9）及式（4-10）得到运动受限机械手在笛卡儿空间的动力学方程为

式中 M^∗——惯性矩阵，M∗＝J^T_qMJ_q^-1；

C^∗＝（J^T_q）^-1CJ_q^-1-（J^T_q）^-1MJ_qJ_q^-1——离心力/哥式力矩阵；

G^∗＝（J^T_q）^-1G——重力；

F_e＝（J^T_q）^-1τ_e——外界对机器人的作用力向量。

本文中采用基于计算力矩的方法进行位置控制，其规则为

F＝M^∗U＋C^∗X＋G^∗＋F_e （4-12）

本文仿真所应用的主要机器人运动学、动力学计算公式代码和参数见第3章与附录。