滑模变结构控制的基本原理^［154］，当系统状态点穿越状态空间的不同区域，达到不连续曲面（滑动超平面）时，控制系统结构随时间变化的开关特性使反馈控制的结构按照一定逻辑切换变化，从而使得系统的状态轨线能够到达期望的滑动超平面，并且沿着这个超平面收敛到原点，这个超平面就是滑模面。系统的动态特性完全由所设计的滑动模态决定，设计适当滑模参数和控制律，系统的状态轨线就能达到期望的平衡点。

一般形式的系统模型

式（4-1）中，状态变量：x∈Rⁿ，t∈R；控制输入：u∈R^m。

定义切换函数s（x）

s（x）＝c₁x₁＋c₂x₂＋…＋c_n-1x_n-1＋x_n （4-2）

这里c₁、c₂、…、c_n-1是确定的系数，在n维向量空间里，式（4-2）确定了一个s（x）＝0的超平面。

对系统表达式（4-1）的滑模变结构控制的问题是求解系统的非连续控制函数(www.daowen.com)

选择u＋（x）和u-（x）使得

当系统处在趋近运动阶段时，要求系统运动必须趋向于滑模面函数s（x）＝0，系统状态必然使滑模面函数满足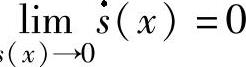。式（4-4）称为滑模面函数s（x）的可达性条件；当s（x）＝0时，系统状态到达滑动超平面，系统沿着此超平面的运动被称为“滑动模态”或简称“滑模”；不连续控制函数式（4-3）就是“滑模变结构控制”函数。

依据上述定义，系统状态在到达滑模面后，即滑动模态下有

c₁x₁＋c₂x₂＋…＋c_n-1x_n-1＋x_n＝0 （4-5）

式（4-5）为系统状态的线性约束。