一般情况下，研磨工具与工件表面之间的关系，表示为空间线段与空间曲面之间的关系（参见图3-13）^［153］。

图3-13 研磨工具与工件表面的空间位姿关系［153］

假设在工件坐标系中工件表面的方程为

F（x，y，z）＝0 （3-20）

研磨工具在工件坐标系中的方程为

式中，x₀、y0、z0为研磨工具接触点P₀（x₀，y₀，z₀）的坐标，而（m，n，p）T为研磨工具的位姿矢量。则P₀点曲面的切面方程为

A（x-x₀）＋B（y-y₀）＋C（z-z₀）＋D＝0 （3-22）其中：

D＝-A·g·x₀-B·g·y₀-C·g·z0(www.daowen.com)

设研磨工具与自由曲面外表面上某点切面的夹角为λ，则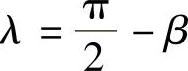（β为研磨姿态角见图3-14），得到

对于给定的待加工自由曲面F（x，y，z）＝0，由第2章得到曲面模型的几何信息，可以计算得出式（3-23）中所需的A、B、C，所以研磨工具与工件曲面在工件坐标空间的位姿矢量（m，n，p）T可以由研磨工具的姿态角β确定。在自由曲面的研磨加工过程中，姿态角β保持恒定，才能保持研磨压力恒定，因为自由曲面上的型值点切平面与其曲率半径相互关联，所以自由曲面自动研磨时，其研磨工具位姿会随着曲面上型值点的曲率半径变化而实时变化。

建立如图3-14所示的工具头刀触点与刀位点关系图，对于自由曲面研磨刀位点（L点）的轨迹，可由刀触点（C点）轨迹数据通过研磨工具头主轴与刀触点公法线的研磨姿态角β计算得到。

C点为工件坐标系中的点，L点为机器人坐标系中的点，建立工件空间坐标到机器人坐标的转换，L点P_l（x_l，y_l，z_l）是由C点P_c（x_c，y_c，z_c）绕x轴旋转研磨姿态角β得到。

图3-14 刀位点与刀触点关系图

化简可得

由此可解决工件坐标系到机器人坐标系的转换。