该系统的拉格朗日能量函数

L＝K-P （3-1）

式中 L——拉格朗日算子；

K——系统的动能；

P——系统的势能。

拉格朗日动力学方程基本表达式为

式（3-2）中 q_i——连杆上某点位置的坐标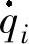；——连杆上某点的速度；

F_i——第i个关节受到的力或者力矩，即机器人动力学所求解的未知量；(www.daowen.com)

n——机器人工具端具有的自由度；

L——系统的动能和势能之差。

系统的动力学模型

式（3-3）中，q为5×1维关节位置矢量，M（q）为5×5维对称正定惯量矩阵，C（q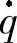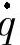，）为5×1维向心力转矩和哥氏力转矩矢量，G（q）为5×1维重力矢量，τ＝（f_xf_yτ_θ3τ_θ4τ_θ5）^T为模型的广义输入力矩。

经过一系列推导和简化运算，机器人动力学方程最终表达式为

式（3-4）中，由于该机器人是五自由度机器人，取n＝5。D_ij称为关节i和j间耦合惯量，因为关节i和j的加速度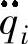和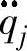将在关节i或j上分别产生一个等于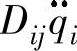或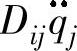的惯性力；如果i＝j，即D_ii表示关节i的有效惯量，因为关节i的加速度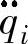将在关节i上产生一个等于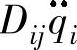的惯性力；I_ai为传动装置的等效转动惯量，对于平动关节，I_ai为等效质量；D_i表示关节i处的重力。

具体计算公式见附录。