本节着重介绍有关离心机生产能力及功率的计算。

（一）上悬式离心机的生产能力计算

上悬式离心机是间歇性操作的，其生产能力除与转鼓的尺寸及机器的性能有关外，还受所分离的糖膏的性质及操作人员的技术熟练程度等因素的影响。

假设转篮的直径为D，高度为H，分离终了时物料层的厚度为100～150mm，如果操作一个周期所需的时间为T，则：

1.人工卸料式离心机

其最大生产能力为：

式中 G_max——最大生产能力，t/d

D——转篮直径，m

d——限料环板的内径，m

H——转篮高度，m

γ——糖膏的重度，kg/m³

T——一个循环周期的时间，min

2.自动卸料上悬离心机

设圆筒部分高为H，圆锥部分高为H₁，则生产能力可用式（11-14）计算：

式中符号意义与式（11-13）同。

自动卸料上悬式离心机在分离一膏时，一个循环周期所包括的阶段时间一般为：

起动至转速为150r/min　　　　　　　 8s

在转速150～300r/min时装料　　　　 20s

自300r/min加速至1000r/min　　　　 48s

正常运转（水洗、汽洗）　　　　　　 85s

关电动机（自1000至300r/min）　　　31s

机械刹车　　　　　　　　　　　　　11s

卸糖　　　　　　　　　　　　　　　25s

最短的工作周期　　　　　　　　　　228s

甜菜糖厂一砂、二砂、三砂糖膏分蜜的操作周期一般为：

一砂糖膏或绵糖膏　　　　　　　　4～6min

二砂糖膏　　　　　　　　　　　　8～10min

三砂糖膏　　　　　　　　　　　　15～30min

为了防止糖膏溢出转篮外，实际装载糖膏的量仅为最大值的95%。换言之，实际生产能力G仅为最大生产能力G_max的95%，即：

国内上悬式离心机已属定型设备，其规格与分离因数均为定值。因此只有缩短操作周期，才能有助于提高生产能力，首先要求晶粒大小整齐均匀，如晶粒大小悬殊，则小晶粒存在于大晶粒之间，堵塞了糖蜜流出的道路，必然延长分蜜的时间；进料应掌握适宜的浓度与温度，这一点对三膏的分蜜尤为重要；此外还须熟练地操作离心机，掌握加速的快慢与制动的时间。所有这些因素对生产能力的提高都有一定的影响。

算得每台离心机的生产能力之后，根据每日所分离各种糖膏的量，不难求得离心机的台数。另外还须外加适当数量的备用离心机。

（二）锥篮式离心机的生产能力计算

目前有关锥篮连续离心机生产能力的一些计算公式还是不够成熟的。下面介绍的是于戈（E·Hugot）在《蔗糖工程手册》中所建议的方法。

连续式离心机的生产能力是以每小时通过离心机的糖膏量来表示的。假如取糖膏的一微元质量为dm，令dm=1，并认为生产能力是与作用在单位质量上的离心力以及总的物质质量所具有的分离面积成正比。

如图11-30所示，垂直于筛面的离心力的分力为：

式中 ω——角速度，1/s

x——质量dm处的回转半径，m

α——半锥角

图11-30 生产能力计算说明图

若分离面积为ds，则生产能力为：

或dG=kω²xcosαds

式中k是与被分离糖膏的性质等因素有关的系数。

位于M平面上半径为x，高度为dh的环形糖膏层。其面积为：

因此

将式（11-18）式沿着锥面从r积分到R，则得生产能力的计算公式为：

根据上述推导过程，式中各符号的单位应为：

式中 G——离心机生产能力，kg糖膏/h

k——比例系数，1/（m²·h）

ω——角速度，1/s

V——锥篮截锥形的体积，m³

α——半锥角

R，r——锥篮大、小端半径，m

由式（11-18）可知，锥篮式离心机的生产能力与锥篮的容积V及角速度的平方ω²成正比。系数k决定于所处理糖膏的黏度、温度以及筛网开孔的百分率；k为有因次的系数，视公式中各项所采取的单位不同而有不同的值。我国生产的几种锥篮式离心机的比例系数k可参考表11-2。

表11-2 锥篮式离心机的比例系数k

若以每天加工甜菜的吨数表示生产能力，则锥篮式离心机的生产能力为

式中 G——生产能力或甜菜加工量，t/d

a——糖膏重量对甜菜百分数

m——锥篮式离心机台数

也可以采用下式计算锥篮式离心机的生产能力：

式中 G——生产能力或甜菜加工量，t/d

a——糖膏重量对甜菜百分数

m——锥篮式离心机台数

f——每台离心机的筛面积，m²

S——分离的糖膏，t/（m²·h），对三砂糖膏取S=3～4t/（m²·h）

【例】某甜菜糖厂有ZhL-1000A锥篮式离心机3台，三砂糖膏重量为甜菜重量的7%，试计算其生产能力（t/d）。

解：因为ZhL-1000A锥篮式离心机的锥篮上端直径为1000m，下端直径为330m，锥角为70°，转速为2000r/min，所以

所以

（一）上悬式离心机的功率计算

上悬式离心机是间歇性生产的，各阶段的运转条件都不一样，因此功率计算是比较复杂的。离心机功率的消耗，一般可包括下列四个方面。

1.启动转鼓的功率N₁

空转篮从静止到转动所消耗的动能为：

式中 E₁——启动转篮所消耗的动能，J

G₀——转篮的质量，kg

ω——转鼓的角速度，1/s

R——转鼓的半径，m

则启动转篮所需的功率N₁为：

式中t₁为转篮起动的时间（s），它与转篮的重量、直径、转数、传动方式及电动机的类型有关，也与操作人员的熟练程度有关。起动时间短，则消耗功率大，但生产能力也大；反之，消耗功率小，生产能力也低。一般t₁在30～120s。设计时往往取较短的起动时间，使设备有一定的潜力。

图11-31 转篮中物料层示意图

2.转动物料所需的功率N₂

由于物料层有一定厚度，在不同厚度处物料的回转半径便不等。现沿着半径为ρ处取一厚为dρ的环形料层（图11-31），则转动所消耗的动能为：

式中 E₂——转动物料所需的动能，J

H——物料层高度，m

γ——料层密度，kg/m³

将式（11-24）从料层半径为r到R处积分，得：

式中 G——料层的质量，kg

其他符号意义同前。

于是转动物料所需的功率N₂为：

式中 t₂——转动物料所使用的时间，s

η——物料的滑动系数，取其值为0.85

3.克服轴承摩擦所消耗的功率N₃

式中 f——轴承的摩擦系数，考虑一定的安全系数而取为0.03

G——转鼓及糖膏的重量，kg

r——轴承处轴颈半径，m

ω——轴的角速度，1/s

4.克服转篮与空气之间摩擦所需的功率N₄

式中 H——转篮高度，m

D——转篮直径，m

n——转篮转速，r/min

α——空气与有孔转篮之间的摩擦系数，取α=1.34×10^-9

间歇式离心机在运转过程中，各阶段所消耗的功率不同，根据经验可采用下列方法计算。

起动加料阶段所需功率N_Ⅰ：

中间阶段所需功率N_Ⅱ：

最后阶段所需的功率N_Ⅲ：

根据各阶段时间的长短，离心机的平均功率为：

分离一砂糖膏：

分离三砂糖膏：

离心机的最大功率为N_max=N_Ⅰ

（二）锥篮式离心机的功率计算

在锥篮式离心机中，所消耗的能量主要是用于克服物料的惯性和移动物料、克服在轴承中的摩擦及转篮与空气间的摩擦。对于Ф650-64°型离心机，其功率消耗包括下列几项。

1.克服物料惯性消耗的功率N₁

因糖膏中晶粒与糖蜜所获得的能量不相同，现分别进行计算。

蔗糖晶粒所消耗的功率：

式中 N_晶——蔗糖晶粒所消耗的功率，W

G_晶——单位时间进入离心机的晶粒重量，kg/s

R——锥篮大端直径，m

ω——锥篮的角速度，1/s

糖蜜所消耗的功率：

式中 N_蜜——糖蜜所消耗的功率，W

G_蜜——单位时间进入离心机的糖蜜重量，kg/s(www.daowen.com)

R₁——糖蜜基本从晶粒中排除的位置，m。一般R₁离锥篮小端直径的距离约为锥篮高的1/3处

则：

2.物料与筛面的摩擦所消耗的功率N₂

式中 N₂——物料与筛面的摩擦所消耗的功率，W

P_料——物料对网面的正压力，N/s

P _料 =G _晶 Rω ² × cosα

f——物料对网面的摩擦系数

f=tanα=tan32°=0. 625

L——锥篮壁的长度，m

3.在轴承中摩擦所消耗的功率N₃

式中 N₃——轴承摩擦所消耗的功率，kW

ρ——轴承上所受的动载荷，kg

f——轴与轴承间的摩擦系数

d——轴颈直径，m

4.锥篮与空气摩擦所消耗的功率N₄

式中 N₄——锥篮与空气摩擦所消耗的功率，kW

D_av——锥篮的平均直径，取几何平均值，D_av=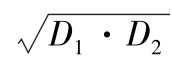，D₁、D₂为锥篮大端、小端的直径，m

H——锥篮高度，m

n——锥篮的转速，r/min

a——系数a=1.34×10^-9

于是功率消耗为：

转篮在运转的过程中，由于转篮本身的离心力及被分离物料作用于篮壁表面的离心压力，使转鼓篮内产生了环向应力。

（一）上悬式离心机转篮的强度计算

若转篮本身的离心力使转篮壁内产生的环向应力为σ₁，而空转篮的离心力为：

F ₀ =G ₀ Rω ² =2πHSγ₀R²ω³

式中 F₀——空转篮的离心力，N

G₀——空转篮质量，kg

R——转篮半径，m

H——转篮高度，m

S——转篮壁厚，m

ω——角速度，1/s

γ₀——转篮材料的密度，kg/m³

于是作用在转篮表面上单位面积的压力为：

在离心力作用下，转篮壁上所产生的环向应力（σ₁）（图11-32）为：

图11-32 转篮壁中应力

由式（11-42）可见，应力σ₁与壁厚S无关，而增大转篮直径及角速度的可能性直接取决于材料的许用应力[σ]。因此对现有的离心机不经强度校核，不应随意提高其工作转速，否则转篮壁将因强度不足而破裂。

糖膏作用在转篮壁面上的离心压力而使壁厚上产生的环向应力为σ₂，而糖膏由于离心力的作用挤压到转篮表面上所造成相应的压强P，其大小为：

式中 P——糖膏对转篮表面的作用压强，Pa

γ——糖膏的密度，kg/m³

R——糖膏外层的半径，m

r——糖膏内层的半径，m

因此在转篮壁内所产生的环向应力为：

于是，转篮壁内所受到的总的环向应力为：

转篮壁因开孔而受到削弱，为保证转篮在运动过程中不致因强度不足而受到破坏，则应保证下列条件，即：

式中 Z——开孔转鼓的削弱系数，其值为Z=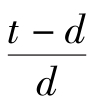_，t为相邻两孔的中心距，d为孔径

[σ]——转鼓材料的许用应力

根据上述公式，可计算转篮的壁厚或校核转篮的强度。但应指出，这只是简易的强度验算，因忽略了整体结构的弯曲力分析。

（二）锥篮式离心机锥篮的强度计算

锥篮在绕轴回转时，由于锥篮本身以及物料作用于其上的离心力，在锥篮壁内也产生了环向力σ₁与σ₂。对于Ф650-64°这一类型式的离心机，可按下列公式进行计算。

令：S——锥篮壁的厚度，m

γ₀——锥篮材料的密度，kg/m³

R′——垂直于母线的篮壁截面处的半径，m

ρ——轴线垂直的锥篮截面处的半径，m（图11-33）

在篮壁上取表面积为A，壁厚为S的单元体积（图11-33）作用于其上的离心力为：

图11-33 锥篮壁应力计算说明图

垂直作用于面积A上的力为：

Fcosα=A·S·γ₀ρω²cosα（N）

则面积A上所受的压强为：

此处锥篮壁内所受到的环向应力为：

而

以R′代入上式得：

可见环向应力在锥篮的大端处（即ρ=R处）为最大，即：

同理，可推导出因为物料作用于锥篮壁表面上的离心压力而产生于壁内的环向应力σ₂为：

式中 γ——糖层密度，kg/m³

δ——糖层平均厚度，m

S——锥篮壁厚，m

此应力σ₂也是在锥篮大端处为最大，即：

于是，锥篮大端处壁内所承受的总的环向应力为σ₁+σ₂，强度校核的条件是：

式中 [σ]为锥篮材料的许用应力。

如果计入面网与衬网所产生于篮壁内的应力，将使计算结果的精确性有所提高。

在设计离心机的轴时，需要特殊考虑的有两方面的问题，一方面是轴的强度计算，另一方面则是轴的临界转速。

（一）轴的强度计算

上悬式离心机及连续锥篮式离心机的轴，主要传递扭矩，根据扭矩进行强度校核。

式中 N——离心机的最大功率，kW

n——离心机的转速，r/min

则轴所受的扭转应力为：

式中 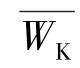——轴的抗扭断面系数

[τ_K]——许用扭转应力，取3.92×10⁷Pa

根据上列公式可计算轴的直径：

对离心机的轴进行强度计算是必要的，但还必须校核离心机轴的临界转速，使离心机在适宜而安全的转速下工作。

（二）轴的临界转速计算

临界转速相应于轴自振频率。在有偏心距时，如果轴的转速与临界转速相等，则其挠度趋于无穷大，便产生了共振，可以从下面的推证来计算轴的临界转速。

对一高速回转的机械，如果转动物体的重心与回转中心不在同一直线上（即存在偏心距），就会产生不平衡离心力而产生振动。如图11-34所示，一个偏心圆盘装在一个重量可忽略不计的轴上，轴支承在两个自位轴承上。圆盘的几何中心为W，而质量重心为S，则e表示圆盘重心S的偏心距。当回转时，轴受到圆盘对其产生的不平衡离心力而被弯曲产生挠度f，同时产生反抗变形的弹性反力P，一直到弹性力与离心力平衡为止。因弹性反力P与挠度f成正比，即：

图11-34 刚性轴的挠度计算说明图

P=af

式中 a为比例系数，与轴的尺寸、材料、力的作用点及轴的固定特性等有关，而轴所受的离心力为：

F=MRω²=M（f+e）ω²

式中 M——圆盘的质量，kg

ω——圆盘的角速度，1/s

f——挠度，cm

e——偏心距，cm

当弹性力与离心力平衡时，

M（f+e）ω²=af

则挠度为：

由式（11-55）可知，随着角速度ω的增加，挠度f也增大，振动将加剧。

当分母a-Mω²=0时，挠度f为无穷大，也就是说，此时轴的转速和轴的自然频率相一致，便产生了共振现象。人们称产生共振时的角速度为临界角速度ω_K，即

与ω_K相应的转速被称为临界转速n_K，则：

根据轴的各种支承特点及圆盘的布置情况，轴的临界角速度值可用表11-3的公式进行计算。

从理论上讲，当轴达到临界转速时，此时挠度为无穷大，轴应被破坏。实际上，如果通过临界转速时进行得相当快，则使轴的挠度来不及达到危险值，同时人们在离心机上设计了减震装置，在通过临界转速时大大地改善了轴的工作条件。

为了保证离心机能平稳地工作，离心机的工作转速应该选择远小于轴的临界转速，实际上如图11-35所示，当工作角速度ω小于0.7倍的临界角速度或者大于1.5倍临界角速度时，轴的工作均能处于正常状态。如

表11-3 各种情况下的临界转速值

图11-35 角速度与挠度的关系图

我们称它为刚性轴。如

我们称它为挠性轴。

当轴的转速处于ω＞6ω_K时，轴的工作反而更趋于平稳，因为此时出现了自动对中现象。

实际上，轴本身是有重量的，而且在大多数情况下所受的载荷不是一个而是几个，所以实际情况要较上述为复杂。

在设计时，采用什么性质的轴将取决于所处理物料的性质及离心机的结构。若选用挠性轴就要设法增加轴的挠性，降低临界转速。采用的措施为：

（1）在满足强度的条件下，轴的直径尽可能取得小些。

（2）轴的长度尽可能长些，使转鼓重心尽量远离轴承的中心。

（3）轴承采用球面支承或弹性支承，使轴在通过临界转速时能降低机器的震动。

（4）转篮应该高些。

如上悬式离心机的轴即是属于挠性结构。

若选用刚性轴，就应该设法增加轴的刚性，使临界转速提高，保证轴在远低于临界转速下工作。采取的措施为：

（1）轴的直径取得大一些。

（2）轴的长度尽可能短一些。

（3）轴承采用固定支承，不允许轴产生摆动。

（4）转篮高度尽可能短些，采用深凹面的筒底，使转篮重心尽可能靠近轴承的中心。

连续式锥篮离心机及三足式离心机的轴都属于刚性轴结构。